[লেখাটি এর আগে পাই জিরো টু ইনফিনিটি ম্যাগাজিনের জানুয়ারি, ২০১৪ সংখ্যায় প্রকাশিত হয়েছিল]

যদিও বাঁধাধরা নিয়ম মানতে আমাদের ভালো লাগে না, তবু নিয়মের মাঝেই রয়েছে গঠনমূলক ফলাফল। আমরা এখানে দেখব ২ থেকে ১১ পর্যন্ত সংখ্যাগুলো দ্বারা  কোন সংখ্যাগুলো বিভাজ্য। আর এই নিয়মটির কাছে হার মানবে TI-89 গ্রাফিক ক্যালকুলেটরসহ বিভিন্ন অনলাইন ক্যালকুলেটর। এমনকি আপনার ক্যালকুলেটরও হার মানতে পারে। একটা ভাগ করেই দেখুন না।

12, 347, 496, 132 কে 11 দিয়ে! আপনার ডিভাইস যদি সংখ্যাটিকে 11 দ্বারা বিভাজ্য দেখায়, তবে ক্যালকুলেটরটি ভুল! কারণ এতে রাউন্ডিং করা হয়েছে, মানে আসন্নীকৃত মান প্রদর্শিত হয়েছে। প্রকৃত ভাগফল হবে 1122499648 দশমিক 3636...36...।

এবার মূল আলোচনায় আসি

বিঃদ্রঃ আলোচনায় বিভাজ্য বলতে নিঃশেষে বিভাজ্য বোঝানো হয়েছে।

২ দ্বারা বিভাজ্য:
আমরা সবাই জানি যে কোনো জোড় সংখ্যাই ২ দ্বারা বিভাজ্য। যেমন, ২, ৮, ১১৪, ৪৩২৫৬ ইত্যাদি।

৩ দ্বারা বিভাজ্য:
কোনো সংখ্যার অঙ্কগুলোর যোগফল যদি ৩ দ্বারা বিভাজ্য হয়, তাহলে সংখ্যাটিও ৩ দ্বারা বিভাজ্য হবে। যেমন ১৪১ এর ক্ষেত্রে ১+৪+১=৬, যা ৩ দ্বারা বিভাজ্য। তাই ১৪১ সংখ্যাটি ৩ দ্বারা বিভাজ্য। কিন্তু যেমন ধরুন ২৩৮ এর ক্ষেত্রে ২+৩+৮=১৩, যা ৩ দ্বারা বিভাজ্য নয়, সুতরাং ২৩৮ তিন দ্বারা অবিভাজ্য। অঙ্কগুলোর যোগফল বেশি বড় হয়ে গেলে (যদি যোগফল দেখে একবারে বোঝা না যায়) যোগফলের জন্যই নিয়মটি আবারও প্রয়োগ করুন।

৪ দ্বারা বিভাজ্যতা:
কোনো সংখ্যার দশক ও এককের ঘরের অঙ্ক নিয়ে গঠিত সংখ্যা ৪ দিয়ে বিভাজ্য হলে সংখ্যাটিও ৪ দ্বারা বিভাজ্য হবে। যেমন ১১৬ এর ক্ষেত্রে ১৬, যা ৪ দিয়ে বিভাজ্য। তাই ১১৬ও ৪ দিয়ে বিভাজ্য। আবার ৫৬০ এর ৬০ যেহেতু ৪ দিয়ে বিভাজ্য, তাই ৫৬০ ও বিভাজ্য।

৫ দ্বারা বিভাজ্যতা:
এটাও আমরা সবাই ভালো করেই জানি এবং কাজে লাগাই। সংখ্যার এককের ঘরের অঙ্ক ০ বা ৫ হলে সেই সংখ্যা ৫ দ্বারা বিভাজ্য। যেমন, ১০৫, ৩০৬০, ৯৬৫ ইত্যাদি।

৬ দ্বারা বিভাজ্যতা: ৬ সংখ্যাটি ২ এবং ৩ এর গুণফল। তাই যে সংখ্যা ২ ও ৩ উভয় সংখ্যা দ্বারা বিভাজ্য হবে, সেটাই ৬ দ্বারা বিভাজ্য হবে। আরো সহজ করে বললে, সংখ্যাটি হবে জোড় এবং অঙ্কগুলোর যোগফল তিন দ্বারা বিভাজ্য হবে। জোড় না হলেই বাদ! জোড় হলেই শুধু তিন এর পরীক্ষা

ব্যাস!

যেমন, ১২০ একটি জোড় সংখ্য এবং তিন দ্বারা বিভাজ্য (কারণ ১+২+০ = ৩)। তাই ১২০ ছয় দ্বারা বিভাজ্য। একইভাবে, ৭৮০ জোড় সংখ্যা এবং ৭+৮+০=১৫, যা ৩ দ্বারা বিভাজ্য, তাই ৭৮০ ছয় দ্বারা বিভাজ্য।

৭ দ্বারা বিভাজ্যতা:
এককের অঙ্ককে বর্গ করে সংখ্যাটির বাকি অংশ থেকে বিয়োগ দিন। ভাগফল ৭ দ্বারা ভাগযোগ্য হলেই কেল্লাফতে!!!

যেমন, ৬৭২ হলে ৬৭-৪=৬৩। সুতরাং $\frac{৬৩}{৭} = ৯।

ইউরেকা! সংখ্যাটি বড় হলে একই প্রক্রিয়ার পুনরাবৃত্তি করা যাবে।

যেমন,  ৪৫১৭৮ হলে ৪৫১৭ - ৬৪ = ৪৪৫৩।
আবার ৪৪৫ - ৯ = ৪৩৬, পুনরায় ৪৩-৩৬ = ৭ যা কাঙ্খিত।

তাই কেল্লাফতে!!!

৮ দ্বারা বিভাজ্যতা: কোনো সংখ্যার সর্বশেষ তিন অঙ্কের সমন্বয়, মানে শতক, দশক ও এককের অঙ্কের সমন্বয় যদি ৮ দ্বারা বিভাজ্য হয়, তাহলে ঐ সংখ্যাটি ৮ দ্বারা বিভাজ্য হয়।
যেমন ৯,৬৪০ আট দ্বারা বিভাজ্য কারণ $\frac{৬৪০}{৮} = ৮০।

তবে এ প্রক্রিয়া ঝামেলাপূর্ণ মনে হতে পারে। কিন্তু ,মনে করুন আপনার কাছে আছে একটি বিশাল সংখ্যা 20,233,322,496। এখন 496 কেই 8 দ্বারা ভাগ দিলেই আপনি বুঝে ফেলবেন রহস্য!

৯ দ্বারা বিভাজ্যতা: তিন এর নিয়মের মতোই অঙ্কগুলোর যোগফল ৯ দ্বারা বিভাজ্য হতে হবে। যেমন ৭,২১৮ এর জন্য ৭+২+১+৮ = ১৮, যা ৯ দিয়ে ভাগযোগ্য।

১০,০০৬,৪৭০ এর জন্য ১+৬+৪+৭=১৮, ফলে এটি ৯ দ্বারা বিভাজ্য হতে বাধ্য।

১০ দ্বারা বিভাজ্যতা: এটাও সবার জানা। মানে এককের ঘরে শূন্য (0) থাকতে হবে।

তবুও নিরস উদাহরণ দিচ্ছি- ১১০, ৭৬০, ১০০৩৭৭৩০ ইত্যাদি।

১১ দ্বারা বিভাজ্যতা: ১১ এর পরীক্ষায় পাস করতে হলে সংখ্যাটির একটার পর একটা পর্যায়ক্রমিক সংখ্যার যোগফল ও বাকী সংখ্যাগুলোর যোগফলের পার্থক্য ১১ দ্বারা বিভাজ্য হতে হবে।
উদাহরণ দেখলে বুঝতে আরেকটু সহজ হবে।

যেমন, ১০৮২৪ এর জন্যে (১+৮+৪) - (০+২) = ১৩ - ২ = ১১।
ফলে, ১০,৮২৪ এগারো দিয়ে বিভাজ্য।

একইভাবে ২৫, ৭৮৪ এর ক্ষেত্রে (২+৭+৪) - ( ৫+৮) = ১৩ - ১৩ = ০ ।

আর ০ ও তো ১১ দিয়ে ভাগ যায় (০ বার!!!)।


এবার তাহলে আলোচনা শুরুর সংখ্যাটির ময়নাতদন্ত করে ফেলি!

সংখ্যাটি হলো 12,347,496,132। সুতরাং (১+৩+৭+৯+১+২) - (২+৪+৪+৬+৩) = ২৩-১৯ = ৪ হয়, মানে ১১ দ্বারা অবিভাজ্য।

দেখা যাচ্ছে এ প্রক্রিয়াটির কাছে যন্ত্র পর্যন্ত আত্মসমর্পণ করেছে!

সূত্র:
১. উহকিপিডিয়া -Division algorithm
২. http://www.mathwarehouse.com/arithmetic/numbers/divisibility-rules-and-tests.php
৩. http://www.mathsisfun.com/divisibility-rules.html

৫০ এর ছোট সব মৌলিক সংখ্যার পরীক্ষা চালাতে এ লিঙ্কে যান। 

Category: articles

Read More...

(লেখাটি এর আগে পাই জিরো টু ইনফিনিটি ম্যাগাজিনে প্রকাশিত হয়)
একবার রাণী ক্যাথেরিনের রাজসভায় দাওয়াত পেয়ে ফ্রেঞ্চ দার্শনিক ডেনিস ডিডেরট তার নাস্তিকপন্থী মনোভাবের জোর প্রচার শুরু করেন। কোন উপায় না দেখে রাণী অয়লারকে ডেকে পাঠান। অয়লার সাহেব এসে ডেনিস সাহেবের সাথে ধর্মীয় আলোচনায় যুক্ত হলেন। অয়লার এক পর্যায়ে বললেন তিনি ঈশ্বরের অস্তিত্বের একটি বীজগাণিতিক প্রমাণ দেখাবেন। ডি মরগানের ভাষ্য মতে ডেনিস সাহেব রাজী হলেন এবং অয়লার পরিপূর্ণ আত্মবিশ্বাস নিয়ে বললেন,

"স্যার, যেহেতু $e ^{i \pi} + 1 = 0$; অতএব ঈশ্বর আছেন।"

রাজসভার সবাইকে হাসার সুযোগ করে দিয়ে গণিতে অপক্ক ডেনিস সাহেব সাথে সাথে প্রস্থান করেন।

এই একটি সমীকরণ গণিতের চারটি শাখার মধ্যে সেতুবন্ধন তৈরি করে। e এর আবির্ভাব ক্যালকুলাস থেকে, π আসে জ্যামিতি থেকে, i এর পদচারণা জটিল সংখ্যার জগতে আর ০ ও ১ এর ব্যবহার পাটিগণিতে। অয়লার মনে করতেন গণিতের সবচেয়ে গুরুত্বপূর্ণ পাঁচটি সংখ্যার এই সম্পর্ক কোনো কাকতালীয় ব্যাপার হতেই পারে না। অতএব ঈশ্বর অবশ্যই আছেন আর তিনিই এই সম্পর্ক গড়েছেন।

এই সংখ্যাগুলো আসলেই একটু স্পেশাল।
এখানে,
e = ন্যাচারাল লগারিদমের ভিত্তি।
π = বৃত্তের পরিধি ও ব্যাসের নির্দিষ্ট অনুপাত
i = কাল্পনিক সংখ্যার একক যার মান √ (-1)
০ = যোগজ অভেদ (Additive Identity)
১ = গুনজ অভেদ (Multiplicative Identity)
এগুলো কেন বিশেষ সংখ্যা তা একটু বলে নেই।

e (অয়লারের সংখ্যা):

গণিতের অন্যতম প্রয়োজনীয় ও গুরুত্বপূর্ণ একটি অমূলদ ধ্রুবক হল অয়লারের সংখ্যা e। এই e হল স্বাভাবিক লগারিদমের ভিত্তি। অর্থ্যাৎ আমরা যাকে লন বা ln বলি (Natural Logarithm) সেটা আসলে loge। এর কাছাকাছি মান হল 2.71828। এটাকে এভাবেও লেখা যায়-

সুইশ গণিতবিদ লিওনার্দ অয়লারের নামে একে e বলা হলেও লগারিদমের আলোচনা করতে গিয়ে জন নেপিয়ার প্রথম e এর ধারণা দিয়েছেন। তাই একে নেপিয়ারের ধ্রুবকও বলা হয়।  এই e কোন র‍্যানডম নাম্বার নয়। ইতিহাসবিদদের মতে, সত্যিকার অর্থে ধ্রুবকটি বের করেছেন কোন বণিক বা ব্যাংকার। কারণ, সংখ্যাটির চক্রবৃদ্ধি সুদের সাথে সম্পর্ক রয়েছে। আরো সূক্ষ্মভাবে বললে, একক প্রাথমিক পরিমাণ থেকে চক্রবৃদ্ধিতে ১০০% হারে এবং অসীম সংখ্যক সময়কালে বর্ধনশীল যেকোনো বৃদ্ধির সর্বোচ্চ মান হতে পারে এই সংখ্যা।

সেমন ধরুন, কোনো পণ্যের দাম ছিল ১ টাকা। ১০০% বৃদ্ধিতে ১ বছরে এর দাম হবে ২ টাকা। [চক্রবৃদ্ধির সূত্রানুযায়ী]
এখন, হার ১০০% ই রেখে একে দুই সময়কালে ভাগ করে নিয়ে প্রতি ছয় মাস পর ৫০% করে বাড়ালে বছর শেষে দাম দাঁড়াবে ২.২৫ টাকা। অর্থ্যাৎ, কিছুটা বেশি । এভাবে সময়কালকে আরো খণ্ডিত করতে থাকলে বছর শেষে পরিমাণও বাড়তে থাকে। কিন্তু যতই বাড়ে ততই বাড়ার হার কমে অর্থ্যাৎ আগের বার তার আগের বারের চেয়ে যতটুকু বেড়েছিল এবার গত বারের চেয়ে তার চেয়ে কম পরিমাণ বেড়েছে। এটা ঠিক যেন মহাবিশ্বের সম্প্রসারণ নীতির বিপরীত যেখানে গ্যালাক্সিরা যতই দূরে সরে, ততই সরে যাবার বেগ বেড়ে যায়।

এখন, এই ক্ষেত্রে প্রথম দিকে অধিক খণ্ডায়ানের প্রতিক্রিয়া বেশি হলেও ধীরে ধীরে এ প্রভাব কমতে কমতে একটি নির্দিষ্ট সংখ্যার কাছকাছি আবর্তিত হয়। সেই সংখ্যাটিই হল 2.718 281 828......, অমূলদ ধ্রুবক।
চক্রবৃদ্ধির সাথে সম্পর্ক থাকার বদৌলতেই ধ্রুবকটি প্রথম কোনো গণিতবিদের হাতে আবিষ্কৃত না হয়ে হয়েছিল ব্যাংকারের হাতে।


পাই(π) 

যে কোনো বৃত্তের পরিধি ও ব্যাসের অনুপাত একটি ধ্রুবক সংখ্যা (π)- এ জ্ঞান চার হাজার বছর প্রাচীন। দূর্ভাগ্যজনক হলেও সত্য এত ন্যাচারাল ও নিরীহ এই ধ্রুবকটিকে দেখলেই এখনও স্কুলপড়ুয়া অনেক শিক্ষার্থী ভয় পায়।  ব্যাবীলনীয় ও মিশরীয়রা ছাড়া আর্কিমিডিস ও চীনের যু চংজি সহ অনেক বিখ্যাত গণিতবিদের গবেষণার খোরাক ছিল এই পাই। অবশেষে ১৭০৬ সালে উইলিয়াম জোন্স পাইকে প্রকাশের জন্য π চিহ্নের প্রস্তাব করেন যাকে ১৭৩৭ সালে কাজে লাগিয়ে বিখ্যাত করেন লিওনার্দ অয়লার। ফ্রেঞ্চ গণিতবিদ জর্জ বুফন সম্ভাব্যতা দিয়ে পাই এর মান বের করার সূত্র বের করেন।

কাল্পনিক সংখ্যার প্রতীক (i):

i হচ্ছে কাল্পনিক সংখ্যা প্রকাশের একক। $i^2 = -1$। কাল্পনিক বলার কারণ হল বাস্তবে এমন কোনো সংখ্যা নেই যার বর্গমূল -1 (মাইনাস 1)। অন্য বাস্তব সংখ্যার মতই অবশ্য -1 এর বর্গমূল দুটি যথা i এবং -i।

শূন্য (০):

0 কে বলা হয় যোগজ অভেদ (Additive Identity)। এটা হল 'নাথিং' বা 'কিছুই না' এর গাণিতিক প্রকাশ।
এটা নিয়ে একটি কৌতুক হল, এক বন্ধু ০ আবিষ্কার করে বলল, "আমি এটা আবিষ্কার করলাম"
২য় বন্ধুঃ কী আবিষ্কার করলে, হে?
১ম বন্ধুঃ কিছুই না!
২য় বন্ধুঃ !!!!!!!!

একে যোগজ অভেদ বলার কারণ, ধরুণ, আপনি ক্রমান্বয়ে অনেক কিছু যোগ করবেন। যখন আপনি কিছুই যোগ করেননি তখন আপনার যোগফল ০। ভাবছেন এ আর এমন কি বিশেষত্ব! হ্যাঁ, বিশেষত্বই বটে। একটু পর বলছি। যাই হোক, একে প্রতিকের বদলে সংখ্যা হিসেবে প্রথম আবিষ্কার করেন ভারতীয়রা।

এক (1) :

১ হল গুণজ অভেদ (Multiplicative Identity)। এর বিশেষত্বের কারণ হল, ধরুন আমরা ক্রমান্বয়ে অনেকগুলো সংখ্যা গুণ করবো। তাহলে যখন একটা গুণও করিনি তখন গুণফল ১। কারণ আদি গুণফল ১ না ধরে ০ ধরলে পরবর্তীতে সব গুণফল হয়ে যাবে ০।  এটা হল এর সাথে যোগজ অভেদের তারতম্য। আর এ কারণেই লজিক্যালি 0! (0 Factorial) এর মান ১ ধরা হয়। অর্থাৎ এখনও কিছুই গুণ করা হয়নি, মানে হাতে মাত্র ১ আছে। কিন্তু 0 Factorial এর মান ০ হলে ফ্যাক্টোরিয়াল নীতিই অস্তিত্ত্ব হারাত, কারণ যে কোনো কিছুর ফ্যাক্টোরিয়াল হত ০।

এ জন্যই যোগ-বিয়োগের ক্ষেত্রে কিছু নেই মানে ০ আর গুণ ভাগের ক্ষেত্রে কিছু নেই মানে ১।
এখন, দেখা যাচ্ছে, এই পাঁচ সংখ্যার আসলেই বিশেষত্ব আছে।

সম্পর্কঃ

$e ^{i \pi} + 1 = 0$

ছোটবেলায় সরল অঙ্কের সরল ফলাফল (এই অর্থে আসলেই সরল!) পেয়ে আমরা কিছুটা হতাশ হতাম বৈকি, এটা তাহলে তার চে' বড় হতাশা! এক দিকে গোবেচারা শূন্য আর অপরদিকে কেমন কিম্ভুতকিমাকার একটি আকৃতি!
এখন চলুন, এটার প্রমাণ দেখে ফেলি-

eiπ = -1 বা $e ^{i \pi} + 1 = 0$ হয় কেন- এই প্রশ্নটির আসল রূপ হচ্ছে আসলে eiπ দ্বারা কী বোঝায়। অর্থাৎ কোনো সংখ্যার ঘাত কাল্পনিক হওয়ার মানে কী? এটা বোঝা গেলেই সমীকরণটিও সরল অঙ্কের মতই সরল হয়ে যাবে।

ডি ময়ভারের সূত্র থেকে আমরা জানতে পারি, সকল x এর জন্য,

এই সমীকরণ থেকে এক্সপোনেনশিয়াল ফাংশনের সাথে ত্রিকোণমিতিক ফাংশনের সম্পর্ক ধরা পড়ে।
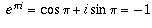তাহলে, x এর বদলে π বসিয়ে আমরা পাই,  । কারণ, cosπ এর মান -1 এবং sinπ এর মান 0।

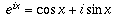এখন কাজ হচ্ছে প্রমাণ করা যে কেন , যেটা থেকে বোঝা যায় e এর ঘাত একটি কাল্পনিক সংখ্যা হবার মানে কী।

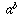সূচকের মৌলিক ধারণা মতে কোনো একটি সংখ্যার ঘাত কাল্পনিক সংখ্যা হওয়া অর্থহীন যেখানে মানে বোঝায় a কে b সংখ্যক বার নিজের সাথে গুণ করা। b ধনাত্মক হলেই কেবল সূচকের এই ধারণা মানানসই হয়। নচেৎ কোন সংখ্যাকে নিজের সাথে i বার (কাল্পনিক সংখ্যক বার) গুণ করার অর্থ কী?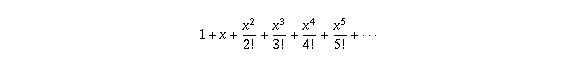

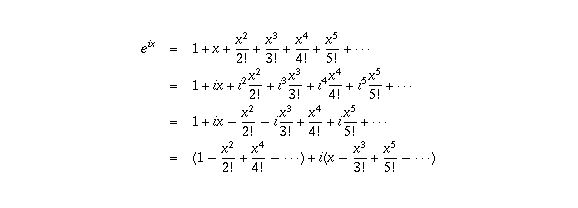
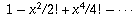অবশ্য সূচকের মূল সংজ্ঞায় b এর মান ভগ্নাংশ কিংবা ঋণাত্মক সংখ্যাও হতে পারে না। কিন্তু এর পরেও কোন সংখ্যার ঘাত ঋণাত্মক বা ভগ্নাংশ হলে আমরা তার থেকে অর্থ বের করে নিতে পারি ।
যেমন, যেহেতু ১/৩ হচ্ছে সেই সংখ্যা যাকে ৩ দ্বারা গুণ করলে ১ পাওয়া যায় সেহেতু a^(1/3) কে অর্থপূর্ণ বলা যাবে এই বলে যে এর ঘাত 3 পর্যন্ত উঠালে a^1 তথা a পাওয়া যাবে।
ফলে, a^(1/3) হচ্ছে a এর ঘনমূল (Cube Root)। একইভাবে ঘাত নেগেটিভ হলে আমরা তারও অর্থ বের করতে পারি। যেমন, a^(-2) মানে 1/(a^2)।

তাহলে একটুখানি ঝামেলা থাকলেও ঘাত ঋণাত্মক বা ভগ্নাংশ হলে আমরা মুশকিলে পড়ি না।
দেখা যাক, কাল্পনিক সংখ্যা যে মুশকিলে ফেলে দেয় তার আসান কোথায়।
তাহলে, আমাদেরকে সূচককে বা তার ধর্মকে এমনভাবে প্রকাশ করতে হবে যাতে এর ঘাত জটিল সংখ্যা বানানো যায়।

এখন, e^x এর ধারাভিত্তিক অসীম সম্প্রসারণ হল- 

যেখানে n! (n factorial) মানে হল ১,....n পর্যন্ত গুণফল। ধারাটি আসে ক্যালকুলাসের টেইলর ধারা থেকে। এখন এই অসীম সমষ্টি জটিল সংখ্যার (যাতে কাল্পনিক সংখ্যা বিদ্যমান থাকে) ক্ষেত্রেও অর্থবহ হয়। আমরা যদি x এর বদলে ix বসাই,
 তাহলে, 
এখন টেইলর সিরিজ আরো বলে যে  হল cosx এর অসীম সমষ্টি এবং  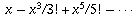হল sinx এর অসীম সমষ্টি। অতএব, ।
সমীকরণটিকে সাজিয়ে লেখা যায় eiπ +1= 0।
ফলে, অনেক জটিল সম্পর্কের সহজ রূপ আমরা পেয়ে গেলাম।সরল ফলাফল!!


তথ্য সূত্রঃ
[১]https://cs.uwaterloo.ca/~shallit/euler.html
[২]http://scidiv.bellevuecollege.edu/Math/Euler.html
[৩]https://www.math.toronto.edu/mathnet/questionCorner/epii.html
[৪]http://arstechnica.com/civis/viewtopic.php?f=24&t=998695
[৫] https://brilliant.org/discussions/thread/the-discovery-of-the-number-e-2/

Category: articles

Read More...

প্যারাডক্স কাকে বলে মনে আছে? যারা ভুলে গেছেন তাদের মনে করিয়ে দেই। সক্রেটিস একবার বলেছিলেন,

‘আমি জানি যে, আমি কিছুই জানি না।‘ 

কথাটায় ভুল আছে। কারণ তিনি যে কিছুই জানেন না- এটা তো অন্তত জানেন। তাহলে কিছুই জানেন না- কথাটা সঠিক নয়। পরে অবশ্য তিনি তাঁর কথা সংশোধন করে বলেছিলেন, 'আমি শুধু এটুকু জানি যে, আমি কিছু জানি না'।

এমন স্ববিরোধী ঘটনা বা বক্তব্যকেই প্যারাডক্স বলে। তবে আবার দেখতে স্ববিরোধী কিন্তু বাস্তবে সঠিক- এমন জিনিসও প্যারাডক্সের কাতারে পড়ে। আজকে আবারও এমন একটি প্যারাডক্স আমরা দেখব।

গ্রিক দার্শনিক জেনো মনে করতেন গতি নিছকই একটি ভ্রম (Illusion), বাস্তব কিছু নয় । মূলত তাঁর অগ্রজ দার্শনিক পারমিনাইডস প্রথম বাস্তবতার দুটি বিপরীত ধারণা তুলে ধরেন। জেনো সাহেব ঐ নীতির সমর্থনেই অনেকগুলো প্যারাডক্স তৈরি করেন। কারণ ভিন্নপন্থীরা পারমিনাইডসের মতবাদের বিরুদ্ধেও তাই করেছিলেন।

জেনোর প্যারাডক্সসমূহের মধ্যে সবচেয়ে বিখ্যাত হলো "একিলিজ ও কচ্ছপ প্যারাডক্স"। আড়াই হাজার বছর আগে জেনোর প্যারাডক্স নিয়ে লেখা বইয়ের এটাই সবচেয়ে সহজে বোঝা যায় যদিও ব্যাখ্যা করা সবচেয়ে দুঃসাধ্য।

প্যারাডক্সটি যা বলতে চায় তা হলঃ

ট্রোজান যুদ্ধের গতিমান বীর একিলিজ (Achilles) কচ্ছপের সাথে রেসে লেগেছেন। কচ্ছপ একিলিজের একটু সামনে। গ্রিক বীর কচ্ছপের চেয়ে অবশ্যই দ্রুতগামী। একটু পেছন থেকে ধাওয়া করে তাকে কচ্ছপকে ওভারটেক করতে হবে। কাজটি সহজই মনে হয়। কিন্তু একটা সমস্যা দাঁড়াল। অতিক্রম করতে হলে আগে বীরকে কচ্ছপ পর্যন্ত পৌঁছতে হবে। একিলিজ যতক্ষণে নিজের ও কচ্ছপের মধ্যকার আদি দূরত্ব পাড়ি দিয়েছেন ততক্ষণে কচ্ছপটি মাঝে আরেকটি গ্যাপ বানিয়ে ফেলেছে। নতুন গ্যাপটি আগের চেয়ে কম, কিন্তু প্রাণিটাকে ধরতে হলে বীরকে সেই দূরত্ব পার হতে হবে। তিনি সেটা করলেনও।

কিন্তু হায়! ততক্ষণে ছোট্ট এই জীবটি আরেকটি নতুন গ্যাপ তৈরি করে ফেলেছে। ফলাফল হল, একিলিজ কখোনোই কচ্ছপকে ধরতে পারবেন না, যত দ্রুতই তিনি গ্যাপ ফিল-আপ করেন না কেন কারণ, কচ্ছপটা বরাবরই নতুন গ্যাপ বানাতে থাকবে। হ্যাঁ, সেগুলো আগেরগুলোর তুলনায় ক্ষুদ্রতর হবে বটে!

একিলিজ ও কচ্ছপের দৌড় প্রতিযোগিতা 

জেনোর যুক্তিকে ভুল বলে উড়িয়ে দেওয়া বেশ লোভনীয়। তবে সাধারণত সেটা করা হয় অলসতা বা অস্বস্তি থেকে। অলসতা- কারণ এটা সমাধান না করেই আমরা সব সময় ভাবতে থাকি, এইতো সমাধান হয়ে গেছে। অস্বস্তির অনুভূতির কারণ হল এতো প্রাচীন এই দার্শনিকের কাছে যুক্তির মার খাওয়া।

এই প্যারাডক্সের উত্তর দিতে গিয়ে অনেকেই বলেন যেহেতু একিলিজের বেগ বেশি তাই তিনি কচ্ছপকে পার হয়ে যাবেন। কিন্তু জেনোতো ধরেই নিয়েছেন আকিলিজের বেগ বেশি। তাই এই বক্তব্য উত্তর হতে পারে না। বেগ বেশি বলেই তো গ্যাপ ক্রমাগত কমছে, কিন্তু কখোনোই জিরো হচ্ছে না।
দর্শন ও গণিতের বেশির ভাগ প্রফেসরদের মতে শুধু এই প্যারাডক্সটি নিয়েই একটা বই লিখে ফেলা যেতে পারে। অনেকে লিখেছেনও।

চলুন, সংক্ষেপে প্যারাডক্সটি ভাঙ্গার চেষ্টা করি।

জেনো প্রমাণ করতে চেয়েছিলেন পরিবর্তন ও গতি বাস্তব কিছু নয়। তাঁর অ্যারো প্যারাডক্সও সেই উদ্দেশ্যেই বানানো।
ইলিনয়েস বিশ্ববিদ্যালয়ের অধ্যাপক নিক হাগেট বলেন জেনোর মত ছিলো,

"গতিকে অস্বীকার করা পাগলামী, তবে মেনে নেওয়া আরো কষ্টকর"।

জগৎ সম্পর্কে আমাদের ধারণা ও বাস্তবতার মধ্যে যে ফারাক প্যারাডক্সটি তাই তুলে ধরে। Enlightening Symbols বইয়ের লেখক ও মার্লবোরো কলেজের গণিতের এমিরিটাস প্রফেসর জোসেফ মাজুরের মতে "প্যারাডক্সটি হচ্ছে এমন যা স্থান, কাল ও গতি সম্পর্কে আমাদেরকে ভুলভাবে চিন্তা করায়"।

তাহলে আমাদের চিন্তার গলদ কোথায়?
গতি বাস্তব এবং সম্ভব, অবশ্যই। আর দ্রুতগামী দৌড়বিদ অবশ্যই কচ্ছপকে হারাবেন। সমস্যাটির সাথে আমাদের ইনফিনিটি বা অসীমতার ধারণার একটি যোগসূত্র আছে। একিলিজের কাজ অসম্ভব মনে হয় কারণ তাকে সসীম সময়ে অসীম সংখ্যক কাজ (গ্যাপ পূরণ) করতে হবে। কিন্তু সব অসীমের প্রকৃতি এক নয়।

ধারাদের মধ্যে অভিসারী (Convergent) ও অপসারী (Divergent) নামক দুই ধরনের ধারা রয়েছে। স্পষ্টতম অপসারী ধারা হল ১+২+৩+... এই ধারার উত্তর অসীম। একিলিজকে এই ধারার ধরণের পথ পাড়ি দিতে হলে কাজটি অসম্ভব হয়ে যেত। অর্থ্যাৎ কচ্ছপ যদি ক্রমান্বয়ে বৃহত্তর দূরত্ব তৈরি করত তখন সেটা অপসারী ধারা হত।

এবার এই ধারাটির কথা ভাবুন $\frac{১}{২}+\frac{১}{৪}+\frac{১}{৮}$+...। অসীম পর্যন্ত চললেও সিরিজটা অভিসারী, যার যোগফল হয় ১। অসীম সংখ্যক পদের যোগফল যে সসীম সংখ্যা হতে পারে এই ধারাটা তার একটি প্রমাণ, যা চমক ভাই কুমড়া থিওরি দিয়ে প্রমাণ করিয়েছিলেন। একিলিজ যদি দ্রুত দৌড়ে ক্রমান্বয়ে দূরত্ব কমান তাহলে যে ধারাটা তৈরি হয় তাও অনেকটা এই ধারাটার মত। ফলে, একিলিজ পরিমাপযোগ্য সসীম সময়ে অসীম ধারা সৃষ্টিকারী দূরত্ব পার হতে পারবেন।

ধারার এই ধারণা জেনোর আরেকটি বিভ্রান্তিকর প্যারাডক্সের জবাব দেয়। সেটা হল দ্বিবিভাজন বা Dichotomy Paradox। মনে করুন, আপনার সামনে একটি বাস আছে, যা আপনি দৌড় দিয়ে ধরতে চাও। মনে করুন, তার দূরত্ব ক। ক দূরত্বে পৌঁছতে প্রথমে আপনাকে $\frac{ক}{২}$ দূরত্বে যেতে হবে। $\frac{ক}{২}$ দুরত্বে যেতে হলে আগে $\frac{ক}{৪}$, $\frac{ক}{৪}$ যেতে $\frac{ক}{৮}$... ইত্যাদি। অর্থ্যাৎ সিকুয়েন্সটা দাঁড়ায় এমন -

{..., $\frac{১}{১৬}, \frac{১}{৮}, \frac{১}{৪}, \frac{১}{২}, ১$}

অর্থ্যাৎ জেনোর মতে যেহেতু বাসটা ধরতে অসীম সংখ্যক পথ পাড়ি দিতে হবে, সেহেতু বাস আর কোন দিনই ধরা হবে না। কিন্তু বেচারা জেনো! অসীম এই ধারা সমষ্টি সসীম। ফলে বাস ধরার স্বপ্নও অধরা থাকবে না।

এ তো আমরা অসীমকে সসীম বানালাম। কিন্তু আরেকভাবে চিন্তা করলে সব সসীমই তো আসলে অসীম। যেমন ধরুন, পরীক্ষার সময় ১ ঘন্টা। এখন, চাইলে এই ঘন্টাকে অসীম সংখ্যক ভাগে বিভক্ত করা যায়। যে কোন রাশিকেই তো ক্ষুদ্রতর এককে হিসাব করতে থাকলে তা ইনফিনিটির দিকে যেতে থাকে।

তবে, প্যারডক্সের রক্ষণভাগ এখোনও ধসেনই। Halfway to Zero বইয়ের লেখক বেঞ্জামিন অ্যালেন এর মতে গাণিতিকভাবে এটা সম্ভব যে একটা দ্রুততর বস্তু একটি কম বেগসম্পন্ন বস্তুকে চিরকাল তাড়া করবে, কিন্তু ধরতে পারবে না, যদি সঠিক প্রক্রিয়ায় দুটোরই বেগ কমতে থাকে।

এরও উত্তর মিলবে দুই ধরণের ধারার পার্থক্যের মধ্যে। $\frac{১}{২}+\frac{১}{৩}+\frac{১}{৪}+\frac{১}{৫}$+... ধারাটিকে অভিসারী মনে হলেও এটা আসলে ডাইভারজেন্ট বা অপসারী (Divergent) । একিলিজ যদি এই ধারার মতো করে কচ্ছপকে তাড়া করে বেড়ায় তবে সত্যি হার মানতে হবে। প্যারাডক্সে তেমন কোনো শর্ত নেই। তাই এবার প্যারাডক্স ঠিকই গোল খেল!

তবে, এই উত্তরে হয়তো গ্রিক দার্শনিকগণ সন্তুষ্ট হতেন না। কারণ, তাদের অনেকেই মনে করতেন চোখে দেখা বাস্তবতার চেয়ে তাদের যুক্তির ক্ষমতা বেশি।

(লেখাটি ইতোপূর্বে পাই জিরো টু ইনফিনিটি ও ব্যাপন ম্যাগাজিনে প্রকাশিত হয়েছে)  

Category: articles

Read More...

ঋণাত্মক সম্ভাবনা!

গণিত ও পরিসংখ্যান সম্পর্কে মোটামুটি ধারণা রাখেন-এমন অধিকাংশ মানুষই কথাটি শুনলে চোখ কপালে তুলে ফেলবেন। ভেংচি কাটবেন। বক্তার মানসিক অবস্থা নিয়ে প্রশ্ন তুলবেন। কারণ তারা জানেন, সম্ভাবনা (Probability) কোনো ঘটনা ঘটার আনুকূল্য প্রকাশ করে। যেমন, কারো কাছে ১০ টি বল আছে। ৫টি বল লাল হলে না দেখে একটি বল তুললে সেটি লাল হবার সম্ভাবনা $\frac{৫}{১০}$। একটিও লাল না হলে লাল বল পাওয়ার সম্ভাবনা $\frac{০}{১০}$ বা শূন্য। সবগুলো লাল হলে সম্ভাবনা হবে $\frac{১০}{১০}$, মানে এক।

অতএব, প্রচলিত ধারণা অনুসারে সম্ভাবনার মান হতে পারে ০ থেকে ১ পর্যন্ত। ০ হলে বোঝা যাবে, ঘটনাটি একেবারেই ঘটবে না। আর ১ হওয়ার মানে, সেটি ঘটবেই। নিশ্চিত। তাহলে সম্ভাবনা আবার ঋণাত্মক হয় কী করে? প্রথাবিরোধী ও অযোৗক্তি চিন্তা!

গণিতের ইতিহাসে কিন্তু এমন বিপরীত চিন্তার প্রাচুর্য লক্ষণীয়। আলেকজান্দ্রিয়ার গ্রিক গণিতবিদ ডায়াফ্যান্টাস বলেছিলেন, 4x + 20 = 0 সমীকরণের যে ঋণাত্মক সমাধান আসে সেটি অযৌক্তিক। ১৭০০ সালেও ইউরোপে ঋণাত্মক সংখ্যাকে অপ্রয়োজনীয় মনে করা হতো। তবে চীন ও ভারতে খ্রিস্টের জন্মের কয়েক শতকের মধ্যেই ঋণাত্মক সংখ্যার প্রচলন ঘটেছিল। ভারতীয়দের সাথে সম্পর্কের সুবাদে ইসলামী আমলের গণিতবিদরাও এর সাথে পরিচিত ছিলেন। কিন্তু শূন্যের মতোই ঋণাত্মক সংখ্যাও ইউরোপে সাধুবাধ পায় অনেক পরে।
এমনকি ১৭৫৯ সালে ইংরেজ গণিতবিদ ফ্র্যান্সিস ম্যাসারস বলেছিলেন,

ঋণাত্মক সংখ্যা একটি সমীকরণের চেহারাকেই কলুষিত করে দেয়। এগুলো একবারেই অর্থহীন।

আঠারো শতকেও সমীকরণের ঋণাত্মক সমাধানকে হিসাবের বাইরে ফেলে দেওয়া হতো। অয়লারের মতো গণিতবিদও এদেরকে অর্থহীন মনে করতেন। শেষ পর্যন্ত লিবনিজ সাহেব এই সংখ্যাদেরকে নিয়মতান্ত্রিকভাবে ব্যবহার করা শুরু করেন।

৪ থেকে ৩ বিয়োগ দিলে ১ হয়। জানি। কিন্তু ৩ থেকে ৪ বিয়োগ দিলে? এর অর্থ তো এমন যে, আমার কাছে তিনটি গরু আছে। সেখান থেকে চারটি গরু আমি কাউকে দিয়ে দিলাম। এটা কীভাবে সম্ভব? ধরুন আমার কাছে ৫০ টাকা আছে। এখান থেকে কি আমি কাউকে ১০০ টাকা দান করতে পারি? হ্যাঁ। তার জন্যে আমাকে প্রথমে ৫০ টাকা ধার করতে হবে। তার মানে ৫০ টাকা থেকে ১০০ টাকা কাউকে দিয়ে দিলে আমার কাছে মাইনাস ৫০ টাকা থাকবে। মানে আমি ৫০ টাকা দেনা থাকব। এভাবেই ঋণাত্মক সংখ্যা বাস্তব হিসাব-নিকাশের অনিবার্য অংশ হয়ে যায়। সহজ করে দেয় গণিতের কাজ।

ঋণাত্মক সংখ্যার মতোই বাধার সম্মুখীন হয়েছিল ভগ্নাংশ ও ’কাল্পনিক’ সংখ্যাও। বর্তমানে এগুলো সুপ্রতিষ্ঠিত গাণিতক সংখ্যা। কোয়ান্টাম মেকানিক্স নামের পদার্থবিদ্যার সবচেয়ে গুরুত্বপূর্ণ ভাগটির শুরুতেই দেখা যায় 'কাল্পনিক' সংখ্যার পদচারণা।

একইভাবে সমূহ সম্ভাবনা দেখা যাচ্ছে ঋণাত্মক সম্ভাবনা নিয়েও। ১৯৪২ সালে নোবেল বিজয়ী তাত্ত্বিক পদার্থবিদ পল ডিরাক একটি পেপার প্রকাশ করেন। এতে তুলে ধরেন ঋণাত্মক সম্ভাবনার কথা। তিনি বলেন,

ঋণাত্মক সম্ভাবনাকে উদ্ভট ভাবা ঠিক নয়। 

১৯৮৭ সালে নোবেলজয়ী আরেক পদার্থবিদ রিচার্ড ফাইনম্যানও এ বিষয়ে একটি পেপার প্রকাশ করেন। তিনি এখানে দেখান, ঋণাত্মক সম্ভাবনার চিন্তা মোটেও আজগুবি নয়। এই ধারণা বরং প্রয়োগ করা যায় পদার্থবিজ্ঞানের অনেকগুলো ক্ষেত্রে।

তাঁর মতে হিসাবের সুবিদার্থে আমরা যেভাবে ঋণাত্মক সংখ্যার ব্যবহার করি, সেই একক যুক্তিতে ব্যবহার করা চলে ঋণাত্মক সম্ভাবনাও। ধরুন, কারো কাছে ১০টি আপেল আছে। এখান থেকে তিনি ১০টি কাউকে দিলেন, আর ৮টি নিলেন কারো কাছ থেকে। ঋণাত্মক সংখ্যা দিয়ে একে সহজেই হিসাব করা যায়। ৫-১০ = -৫ এবং -৫+৮ = ৩। শেষ পর্যন্ত সন্তোষজনকভাবে ধনাত্মক সংখ্যাই পাওয়া গেল। যদিও মাঝখানে ব্যবহার করা হয়েছে 'অযৌক্তিক' ঋণাত্মক সংখ্যা।

এবার মনে করুন, তিনটি তল বিশিষ্ট একটি গুটিতে যথাক্রমে ১,২ ও ৩ লেখা আছে। আরও ধরুন, গুটিগুলোকে দুইটি ভিন্ন শর্ত মেনে নিক্ষেপ করা যাবে। শর্ত A ও শর্ত B। শর্ত দুটির ক্ষেত্রে সম্ভাবনার মান হবে আলাদা। ধরুন, শর্ত A-এর ক্ষেত্রে ১ পড়ার সম্ভাবনা $P_{1A}$ = ০.৩, ২ পড়ার সম্ভাবনা $P_{2A}$= ০.৬ এবং ৩ পড়ার সম্ভাবনা  $P_{3A}$ = ০.১। শর্ত B-এর ক্ষেত্রে সম্ভাবনাগুলো যথাক্রমে $P_{1B}$ =০.১, $P_{2B}$= ০.৪ ও $P_{3B}$ = ০.৫। তার মানে, বিষয়টা এ রকম:

অবস্থা	শর্ত A	শর্ত B
০১	০.৩	০.১
০২	০.৬	০.৪
০৩	০.১	০.৫
মোট	১	১

এবার ধরুন গুটিটিকে মোট ১০ বার নিক্ষেপ করা হলো। ৭ বার নিক্ষেপ করা হলো শর্ত A অনুসারে। বাকি ৩ বার শর্ত B অনুসারে। তার মানে A-এর সম্ভাবনা P$_A$= ০.৭ ও B-এর সম্ভাবনা P$_B$= ০.৩। মনে রাখতে হবে, একটি সিস্টেমের সবগুলো ঘটনা ঘটার মোট সম্ভাবনা এক (১) হবে। এখন গুটি নিক্ষেপ করে সম্ভাবনার তত্ত্ব অনুসারে ১ পাওয়ার সম্ভাবনা হবে ০.৭ × ০.৩ + ০.৩ ×০.১ =০.২৪।

তার মানে, a যদি শর্ত হয়, আর P$_{ia}$ যদি হয় শর্তাধীন সম্ভাবনা, তাহলে a শর্তের জন্যে i এর সম্ভাবনা হবে
P$_i$ = $\sum_aP_{ia}.P_a$
এখানে P$_a$ হলো a শর্ত পূরণ হবার সম্ভাবনা। P$_{ia}$ মানে হলো i ও a ঘটার যৌথ সম্ভাবনা। বুঝতে অসুবিধা হলে টেবিল থেকে মিলিয়ে নিন। যেহেতু প্রতিটি শর্তের জন্যে কিছু না কিছু ঘটবেই, তাই $\sum_iP_{ia}$ =1 হবে।
যদি কোনো একটি শর্ত অবশ্যই পূরণ হয়, তাহলে যদি $\sum_aP_a$---(১)
হয় তাহলে $\sum_iP_i$ হবে।

(১) অনুসারে, আমরা কোনো না কোনো ফলাফল পাবই।

এবার ধরুন, কিছু শর্তাধীন সম্ভাবনা ঋণাত্মক হলো। ঋণাত্মক সংখ্যার মতোই ফাইনাল ফলকে অযৌক্তিক না বানিয়ে আমরা মাঝখানে এর ব্যবহার করতে পারি কি না দেখা যাক। এবার টেবিলটা এ রকমঃ

অবস্থা	শর্ত A	শর্ত B
০১	০.৩	-০.৪
০২	০.৬	১.২
০৩	০.১	০.২
মোট	১	১

টেবিলটা এমনভাবে করা হয়েছে যাতে (১) অনুসারে $P_{1B}$+ $P_{2B}$+ $P_{3B}$=1  হয়। এবার তাহলে ১ পাওয়ার সম্ভাবনা হবে $P_1$ = ০.৭×০.৩+০.৩× (-০.৪) =০.৯। স্বাভাবিক ফল। $P_{2B}$ ও ১ এর বেশি (১.২) হয়েছে। এ ধারণার সাথে ঋণাত্মক সম্ভাবনার কোনো পার্থক্য নেই। এটি হলো ঘটনাটি না ঘটার ঋণাত্মক সম্ভাবনা।

একইভাবে হিসাব করে ২ ঘটার সম্ভাবনা পাওয়া যাবে $P_2$=০.৭×০.৬+০.৩×১.২ =০.৭৮।

৩ ঘটার সম্ভাবনা হবে $P_3$=০.১৩। এদের যোগফল হয় ১, যা স্বাভাবিক ফল। আবার শর্তগুলোর নিজেদের অথবা ১, ২ বা ৩ ঘটার সম্ভাবনাও ঋণাত্মক হতে পারে। তবুও ফাইনাল রেজাল্ট যৌক্তিক হওয়া সম্ভব।

তাহলে ঋণাত্মক সম্ভাবনাকে আমরা ফাইনাল রেজাল্টের জন্যে স্বাভাবিক হিসেবে মেনে না নিলেও অন্তত হিসাবের সুবিদার্থে মাঝখানে ব্যবহার করতেই পারি। এতে সম্ভাবনা তত্ত্বের কোনো বিধানের বিরুদ্ধে যাওয়া হয় না। ফাইনম্যান তাঁর পেপারে ঋণাত্মক সম্ভাবনার কিছু ব্যবহারিক উদাহরণও দেখিয়েছিলেন।

ইদানিং এ বিষয়ে নিয়মিত পেপার আসছে। মার্ক বারগিন ২০১০ সালে এক পেপারে এর প্রয়োগ দেখাতে গিয়ে একটি সুন্দর উদাহরণ দিয়েছেন। মনে করুন, আমি কোনো বানান ভুল করি না। তাহলে এ লেখায় 'কারন' ('কারণ' এর স্থলে) শব্দটি থাকার সম্ভাবনা কত? প্রচলিত সম্ভাবনা সূত্র অনুসারে উত্তর হবে ০। কিন্তু অনেক সময় টাইপিং-এ ভুল হয়। অতএব আমরা বলতে পারি, লেখায় 'কারন' শব্দটি থাকার সম্ভাবনা হবে (-০.১)। পরে এটি ঠিক করা হলে আর কোনো ভুল বানান থাকবে না। অর্থাৎ, বলা যায়, টাইপিং ভুলের আগে সম্ভাবনা ঋণাত্মক ছিল। সব ভুল দূর করার পরে সম্ভাবনা শূন্য হলো।

১৯৩২ সালে আরেক নোবেল বিজয়ী ইউজিন উইগনারও ঋণাত্মক সম্ভাবনার দেখা পান। ১৯৪৫ সালে ইংরেজ পরিসংখ্যানবিদ  মরিস বার্টলেট দেখান, ঋণাত্মক সম্ভাবনার মধ্যে কোনো গাণিতিক বা যৌক্তিক অসঙ্গতি নেই। ২০১০ সালে এস্পেন হউগ দেখান যে গাণিতকি অর্থনীতিতেও এই ধারণা কাজে লাগানো সম্ভব।

সূত্রঃ
1. http://cds.cern.ch/record/154856/files/pre-27827.pdf
2. https://betterexplained.com/articles/a-visual-intuitive-guide-to-imaginary-numbers/
3. https://en.wikipedia.org/wiki/Negative_number#First_usage_of_negative_numbers

Category: articles

Read More...