কাজটা করার অনেকগুলো উপায় আছে। সবচেয়ে ভালো উপায় হলো readxl প্যাকেজ ব্যবহার করা। তবে এমন যদি হয় যে শুধু অল্প কিছু ডেটা লাগবে, মানে অল্প কয়টি row আর কলাম, তাহলে? এক্ষেত্রে প্যাকেজ ব্যবহার করে করা বা ফাইলকে csv বানিয়ে কাজ করা বেশ সময়সাপেক্ষ। আমরা চাই ১ সেকেন্ডে করে ফেলতে।

যেমন ধরুন, আমরা এ রকম একটা এক্সেল ডেটাকে R-এ নিয়ে আসতে চাই।

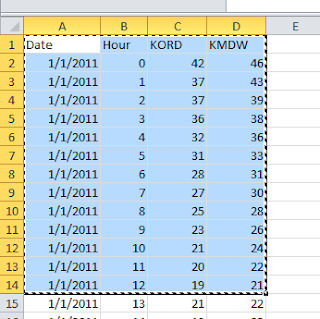এক্সেল ডেটা 

প্রথমেই আমরা R-এ সামান্য একটু কাজ করে রাখি। নীচের ফাংশনটি এক্সিকিউট করাতে হবে।

excelr <- function(header=TRUE,...) {
  read.table("clipboard",sep="\t",header=header,...)
}

এই ফাংশনটা কিন্তু বারবার রান করাতে হবে না। এক সেশনে বা Rstudio এর এক প্রোজেক্টে একবার রান করালেই হবে। আর অবশ্যই excelr এর বদলে R এর নিয়ম মেনে যে-কোনো নাম দিতে পারেন। নামটা মনে রাখলেই হবে।

এবার এক্সেলে গিয়ে নির্দিষ্ট অংশটিকে হাইলাইট করে কপি করতে হবে। রাইট ক্লিক দিয়ে copy বা ctrl + C চাপুন। এটা তাহলে কম্পিউটারের ক্লিপবোর্ডে থাকবে।

এবার R-এ এসে নীচের কোড রান করার। যতবার কপি করা দরকার হবে, শুধু এক্সেলে কপি করে এটা রান দিলেই কেল্লাফতে!

new_data <- excelr()

ব্যস! এক্সেলের ডেটাটুকু new_data নামে একটি ডেটাফ্রেইমে সেইভ হয়ে যাবে। তবে মনে রাখতে হবে, শুরুতে ফাংশনের নাম যেটা দিয়েছেন এখানেও সেটাই দিতে হবে।

চাইলে Rstudio তে View() ফাংশন কাজে লাগিয়ে দেখে নিতে পারেন কী পেলেন!

নিশ্চয়ই ভাবছেন, তাহলে উল্টো কাজটা কীভাবে হবে? R থেকে এক্সেলে কীভাবে নেব? এটাও আগেরটার মতোই সহজ কাজ। মনে করুন, আপনি my_data অংশটিকে এক্সেলে নিয়ে যেতে চান। তাহলে আগের মতোই আগে একটা ফাংশন রান করে রাখুন।

write.excel <- function(x,row.names=FALSE,col.names=TRUE,...) {  write.table(x,"clipboard",sep="\t",row.names=row.names,col.names=col.names,...)

}

এবার রান করুন
write.excel(dat)

এবার এক্সেলে গিয়ে Ctrl+V চাপুন। বা মাউসে রাইট ক্লিক করে paste অপশনে ক্লিক করুন। আবার চাইলে এটাকে সরাসরি ওয়ার্ড ফাইলেও পেস্ট করতে পারেন।

 সূত্র
১। R-Bloggers

Category: articles

Read More...

মনে করুন, এমন একটি জরিপ চালানো হলো, যেখানে মানুষের আয়, বয়স, শিক্ষাগত যোগ্যতা, লিঙ্গ, ধর্ম ইত্যাদি অনেকগুলো চলক (variable) নিয়ে তথ্য সংগ্রহ করা হল। আরও ধরা যাক, কাজটি করা হলো অনেকগুলো আলাদা আলাদা সময়ের জন্য। এভাবে পাওয়া ডেটাকেই আমরা বলব প্যানেল ডেটা। অর্থাৎ, যেখানে অনেকগুলো আলাদা আলাদা চলক সম্পর্কে আলাদা আলাদা সময়ের বিচারে তথ্য নেওয়া হবে সেটাই হবে প্যানেল ডেটা (panel data)।

প্যানেল ডেটার একটি উদাহরণ দেখুন:
\begin{array}{|c|c|c|c|c|}
\hline
person & year & income& age & gender\\ \hline
1&2001& 24000&28 &male\\ \hline
1& 2002& 24500 & 29&male\\ \hline
1&2003 & 28000&30&male\\ \hline
2&2001& 34000&35 &male\\ \hline
2& 2002& 37500 &36&male\\ \hline
2&2003 & 40000&37&male\\ \hline
3&2001& 40000&40 &male\\ \hline
3& 2002& 45500 &41&male\\ \hline
3&2003 & 50000&42&male\\ \hline
\end{array}
প্যানেল ডেটার আরেক নাম লনজিটিউডিনাল (longitudinal) ডেটা।

এবার তাহলে ক্রস-সেকশনাল (cross-sectional) ও টাইম সিরিজ (time series) ডেটা বুঝে নেওয়া যাক।

একই চলকের তথ্য যখন বিভিন্ন সময়ে নেওয়া হবে তখন সেটাই হয়ে যাবে টাইম সিরিজ ডেটা। 

টাইম সিরিজ ডেটা বা কালীন সারির একটি উদাহরণ:
\begin{array}{|c|c|}
\hline
year & income\\ \hline
2001& 24000\\ \hline
2002& 24500\\ \hline
2003& 25000\\ \hline
2004& 27000\\ \hline
2005& 28000\\ \hline
2006& 30000\\ \hline
2007& 33000\\ \hline
2008& 33400\\ \hline
2009& 35000\\ \hline
2010& 45000\\ \hline
2011& 46000\\ \hline
2012& 46800\\ \hline
2013& 50000\\ \hline
2014& 55000\\ \hline
2015& 67000\\ \hline
\end{array}
আবার একটি নির্দিষ্ট সময়ে যখন অনেকগুলো আলাদা চলকের তথ্য নেওয়া হবে, সেটা হয়ে যাবে ক্রস-সেকশনাল ডেটা। যেমন আমাদের প্রথম টেবিলে আমরা যদি প্রত্যেক person এর জন্য শুধু ২০০১ সালের ডেটা চিন্তা করি, তাহলে সেটা ক্রস-সেকশনাল ডেটা হবে। একইভাবে শুধু ২০০২ বা ২০০৩ চিন্তা করলেও একই কথা। কিন্তু একই সাথে একাধিক সময় বিবেচনায় নিলেই সেটা হয়ে যাবে প্যানেল ডেটা।

একটি সহজ বিষয়। একদম উপরের টেবিলটার কথা ভাবুন। এখান থেকে একটি কলাম আর সাথে বছর- এই দুটি চলক নিয়ে নতুন একটি ডেটাসেট তৈরি করলেই সেটা হবে টাইম সিরিজ ডেটা। তবে একাধিক ব্যক্তির জন্য চিন্তা করলে, মানে একই বছর একাধিক বার নিলে সেক্ষেত্রে দুটো আলাদা টাইম সিরিজ ডেটা হবে।

আবার ঐ টেবিলেই কলামের পরিবর্তে একটি সারি (row) নিয়ে নিলে (সাথে টেবিলের হেডার, যেখানে আছে চলকগুলোর নাম) পাওয়া যাবে ক্রস-সেকশনাল ডেটা। অনেকগুলো সারি নিলেও সমস্যা নেই, যদি না আলাদা আলাদা সময় চলে আসে।

ক্রস-সেকশনাল ডেটার উদাহরণ
\begin{array}{|c|c|c|c|c|c|c|}
\hline
person & year & income& age & gender&height (cm)&weight(kg)\\ \hline
1&2001& 24000&28 &male&172&76\\ \hline
2&2001& 34000&35 &male&171&81\\ \hline
3&2001& 40000&40 &male&165&65\\ \hline
\end{array}
ডেটার উপর ভিত্তি করেই আবার অ্যানালাইসিসির নাম হয়। যেমন প্যানেল ডেটা নিয়ে কাজ করলে বলা হয় প্যানেল অ্যানালাইসিস। টাইম সিরিজ ডেটা নিয়ে টাইম সিরিজ অ্যানালাইসি। আবার দুটোর সমন্বয় নিয়ে হতে পারে ক্রস-সেকশনাল স্টাডি। আবার উল্টোটাও হয়। স্টাডি কেমন হবে সেটার উপর নির্ভ করে সংগ্রহ করা হয় ডেটা। প্রতিটি স্টাডিরই কিছু সুবিধা-অসুবিধা আছে।

এ বিষয়ে বিস্তারিত জানতে নীচের বইগুলো সহায়ক হতে পারে:

১। Fitzmaurice, Garrett M.; Laird, Nan M.; Ware, James H. (2004). Applied Longitudinal Analysis. Hoboken: John Wiley & Sons. p. 2.
২। Epidemiology for the Uninitiated by Coggon, Rose, and Barker, Chapter 8, "Case-control and cross-sectional studies", BMJ (British Medical Journal) Publishing, 1997
৩। Baltagi, Badi H. (2008). Econometric Analysis of Panel Data (Fourth ed.). Chichester: John Wiley & Sons.
৪। Diggle, Peter J.; Heagerty, Patrick; Liang, Kung-Yee; Zeger, Scott L. (2002). Analysis of Longitudinal Data (2nd ed.). Oxford University Press. p. 2.

Category: articles

Read More...

[স্টিফেন হকিং এর লেখা ও আব্দুল্যাহ আদিল মাহমুদ অনূদিত অ্যা ব্রিফার হিস্ট্রি অব টাইম বই অবলম্বনে]  

বিজ্ঞানী হতে হলে জানতে হবে বিজ্ঞান বা বৈজ্ঞানিক তত্ত্ব কাকে বলে।

সোজা কথায় বললে, থিওরি বা তত্ত্ব হচ্ছে একটি মডেল বা নমুনা, অথবা সেই নমুনার কোন সীমিত অংশবিশেষ এবং এমন এক গুচ্ছ নিয়ম বা সূত্র, যে সূত্রগুলো পর্যবেক্ষণে প্রাপ্ত তথ্যকে মডেলের মাধ্যমে ব্যাখ্যা করতে পারবে। এই তত্ত্ব থাকে আমাদের মস্তিষ্কে এবং এর অন্য রকম কোনো বাস্তবতা নেই (বাস্তবতার সংজ্ঞা যা হয় হোক)।

একটি তত্ত্বকে ভালো বলা হয় যদি এর মধ্যে দুটো গুণ পাওয়া যায়। এক, অনেকগুলো পর্যবেক্ষণকে এটি অল্প কথায় সঠিকভাবে ব্যাখ্যা করতে পারবে। দুই, একে ভবিষ্যত পর্যবেক্ষণের ফলাফল সম্পর্কে সুনির্দিষ্ট পূর্বাভাস [১] দিতে হবে। অ্যারিস্টটল এমপেডোক্লেসের এই তত্ত্ব  মেনে নিয়েছিলেন যে জগতের সবকিছু মাটি, বায়ু, আগুন ও পানি- এই চারটি উপাদান দিয়ে তৈরি। তত্ত্বটি যথেষ্ট সরল ছিল, কিন্তু এটি কোনো সুনির্দিষ্ট পূর্বাভাস দিতে পারেনি। অন্য দিকে, নিউটনের মহাকর্ষ তত্ত্বটি উপস্থাপন করা হয় আরো সরল ভাবে। এই তত্ত্বে বস্তুরা একে অপরকে তাদের ভরের সমানুপাতিক ও তাদের মধ্যবর্তী দূররত্বের বর্গের ব্যস্তানুপাতিক বলে আকর্ষণ করে। তত্ত্বটি দেখতে সরল হলেও এটি অনেক নিখুঁতভাবে সূর্য, চন্দ্র এবং গ্রহদের গতির পূর্বাভাস দিতে পারে।

যে কোনো ভৌত তত্ত্বই (physical theory)এই অর্থে অস্থায়ী যে এটি শুধুই একটি অনুমান। একে কখোনই পুরোপুরি প্রমাণ করা যাবে না। পরীক্ষার ফলাফলের সাথে হাজারবার মিলে গেলেও আপনি কখোনই নিশ্চিত করে বলতে পারবেন না এটি পরের বার বিপরীত ফলাফল দেবে না। উল্টো দিকে একটি তত্ত্বকে ভুল বলার জন্যে এর বিপক্ষে একটি মাত্র পর্যবেক্ষণই যথেষ্ট। বিজ্ঞানের দার্শনিক কার্ল পপার যেমন জোর দিয়ে বলেছেন,

একটি ভালো তত্ত্বের বৈশিষ্ট্য হচ্ছে, এতে এমন অনেকগুলো পূর্বাভাস থাকবে যাদেরকে পর্যবেক্ষণের মাধ্যমে ভুল বা মিথ্যা প্রমাণ করার সুযোগ থাকবে। 

যখনি নতুন কোনো পরীক্ষার সাথে এর পূর্বাভাস মিলে যাবে, তত্ত্বটি বেঁচে যাবে। কিন্তু কখনো নতুন কোনো পর্যবেক্ষণ এর সাথে না মিললে আমাদেরকে তত্ত্বটিকে পরিত্যাগ বা সংস্কার করতে হবে।

বাস্তবে দেখা যায় নতুন তত্ত্ব আসলে আগের তত্ত্বেরই পরিবর্ধন মাত্র। উদাহরণ হিসেবে বলা যায় বুধ গ্রহের গতির কথা। নিউটনের মহাকর্ষ তত্ত্বের পূর্বাভাসের সাথে এর গতির সামান্য ভিন্নতা দেখা দেয়। আইনস্টাইনের সার্বিক আপেক্ষিক তত্ত্ব নিউটনের তত্ত্বের চেয়ে কিছুটা ভিন্ন অনুমান প্রদান করে, যা পর্যবেক্ষণের সাথে ঠিক ঠিক মিলে যায়। নিউটনের তত্ত্বের জায়গায় নতুন এই তত্ত্বের জায়গা করে নিতে এটি গুরুত্বপূর্ণ ভূমিকা রাখে। তবু এখনও আমরা বাস্তবে নিউটনের তত্ত্বই বেশি ব্যবহার করি, কারণ আমাদের দৈনন্দিন জীবনের প্রয়োজনীয় ক্ষেত্রে দুটো থিওরির পার্থক্য সামান্য। নিউটনের তত্ত্বের আরেকটি সুবিধা হল এটি আইনস্টাইনের সূত্রের চেয়ে অনেক সরল।

বিজ্ঞানের চূড়ান্ত লক্ষ্য হচ্ছে এমন একটি তত্ত্ব প্রদান করা,  যা সমগ্র মহাবিশ্বকে ব্যাখ্যা করতে পারবে। অবশ্য অধিকাংশ বিজ্ঞানীই বাস্তবে সমস্যাটিকে দুই ভাগে বিভক্ত করে কাজ করেন। প্রথমত, কিছু সূত্র আমাদেরকে বলছে যে সময়ের সাথে সাথে মহাবিশ্বের কীরূপ পরিবর্তন ঘটছে। (আমরা যদি কোনো একটি সময়ে মহাবিশ্বের অবস্থা জানি, এই ভৌত সূত্রগুলো আমাদের বলবে পরবর্তী কোনো সময়ে মহাবিশ্ব কী অবস্থায় থাকবে।) দ্বিতীয় প্রশ্নটি হল মহাবিশ্বের আদি অবস্থা নিয়ে। কেউ কেউ মনে করেন, বিজ্ঞানের উচিত শুধু প্রথম অংশটি নিয়ে কাজ করা। তাদের মতে, মহাবিশ্বের আদি অবস্থার বিষয়টি অধিবিদ্যা[২] বা ধর্মের আলোচ্য বিষয়। তাদের মতে, সর্বশক্তিমান ঈশ্বর মহাবিশ্বের সূচনা নিজের যেভাবে ইচ্ছা সেভাবেই করেছেন[৩]। তা হলেও হতেও পারে, কিন্তু সেক্ষেত্রে ঈশ্বর মহাবিশ্বকে কোনো অনির্দিষ্ট প্রক্রিয়াতেই বিবর্তিত হতে দিতেন। কিন্তু বাস্তবে দেখা যাচ্ছে তিনি একে কিছু নির্দিষ্ট নিয়মের অধীন করেছেন, যা কিছু সূত্র মেনে চলছে। কাজেই মহাবিশ্বের আদি অবস্থাও কিছু নিয়ম মেনে চলছিল মনে করাটাই যুক্তির দাবি।

মহাবিশ্বের সবকিছুকে একই তত্ত্বে গেঁথে ফেলা কঠিন একটি কাজ। ফলে আমরা একে ভেঙে অনেকগুলো আংশিক তত্ত্ব তৈরি করি। এই আংশিক তত্ত্বদের প্রতিটি কিছু নির্দিষ্ট পর্যবেক্ষণের ব্যাখ্যা ও পূর্বাভাস দিতে পারে। এর আওতার বাইরের বিষয়গুলো সম্পর্কে এটি নীরব থাকে অথবা তাদেরকে কিছু সংখ্যা দ্বারা প্রকাশ করে। খুব সম্ভব, এটি একটি ভুল পদ্ধতি। যদি মৌলিক জায়গাটিতে মহাবিশ্বের সবকিছু অন্য সব কিছুর উপর নির্ভরশীল হয়, তাহলে এদেরকে আংশিকভাবে মূল্যায়ন করে পূর্ণাঙ্গ সমাধানে পৌঁছা সম্ভব নাও হতে পারে। তবুও, আমরা অতীতে কিন্তু এটাই করে এসেছি।

উদাহরণ হিসেবে আবারও বলব নিউটনের মহাকর্ষ তত্ত্বের কথা। এটি বলছে, দুটো বস্তুর মধ্যে ক্রিয়াশীল মহাকর্ষ বল বস্তুদ্বয়ের একটিমাত্র নিজস্ব বৈশিষ্ট্যের উপর (ভর)নির্ভরশীল[৪]। বস্তু কী দিয়ে তৈরি তার উপর এই বল নির্ভর করে না। কাজেই গ্রহদের কক্ষপথের হিসাব বের করার জন্য এদের এবং সূর্যের গঠন ও উপাদানের জন্যে আমাদের আলাদা কোনো তত্ত্বের প্রয়োজন নেই।

বর্তমানে মহাবিশ্বের ব্যাখ্যায় বিজ্ঞানীরা দুটি মৌলিক আংশিক তত্ত্ব কাজে লাগাচ্ছেন। এরা হল জেনারেল থিওরি অব রিলেটিভিটি বা সার্বিক আপেক্ষিক তত্ত্ব ও কোয়ান্টাম মেকানিক্স। এই দুটি তত্ত্ব বিংশ শতাব্দীর প্রথমার্ধের বুদ্ধির জগতের এক বিরাট অর্জন। সার্বিক আপেক্ষিক তত্ত্ব মহাকর্ষ বল ও মহাবিশ্বের বড় দৈর্ঘ্যের কাঠামোকে (Large scale structure) ব্যাখ্যা করে। মাত্র কয়েক মাইল থেকে শুরু করে অন্তত এক হাজার কোটি কোটি কোটি (১ এর পরে ২৪ টি শুন্য) মাইল তথা পর্যবেক্ষণযোগ্য মহাবিশ্বের আকারের সমপরিমাণ অংশ এই তত্ত্বের আওতায় আছে। অন্য দিকে কোয়ান্টাম মেকানিক্স কাজ করে এক ইঞ্চির এক লক্ষ কোটি ভাগের এক ভাগের মতো অত্যন্ত ক্ষুদ্র দৈর্ঘ্যের জগতে।

পরমাণু থেকে মহাবিশ্ব। [বিংশ শতকের প্রথমার্ধ পর্যন্ত নিউটনীয় পদার্থবিদ্যার সূত্রগুলো কাজ করত শুধু দৈনন্দিন জীবনের ক্ষেত্রগুলোতে। এরপরে এসে পদার্থবিদ্যার পরিধি বিস্তৃত হয়ে পৌঁছায় মহাবিশ্বের ক্ষুদ্রতম থেকে বৃহত্তম চৌহদ্দি পর্যন্ত। ] 

এই দুটি তত্ত্ব আবার একে অপরের বিরোধী- এদের দুটোই যে ঠিক হবে সেটি সম্ভব নয়। বর্তমানে পদার্থবিদ্যার একটি প্রধান লক্ষ্য হচ্ছে নতুন একটি তত্ত্ব প্রদান করা, যা এই দুটো তত্ত্বকে একীভূত করে কোয়ান্টাম গ্র্যাভিটি নামে কমন একটি তত্ত্বের জন্ম দেবে। এখনও এমন তত্ত্ব প্রস্তুত করতে হয়নি। হতে পারে, আমরা এখনও এর থেকে বহু দূরে আছি। কিন্তু এই তত্ত্বের কী কী বৈশিষ্ট্য থাকা উচিত তার অনেকগুলোই ইতোমধ্যে জানা সম্ভব হয়েছে।

এখন আমরা যদি বিশ্বাস করি যে মহাবিশ্ব এলোমেলোভাবে নয় বরং চলছে কিছু নির্দিষ্ট নিয়ম মেনে, তাহলে এই আংশিক সূত্রগুলোকে অবশ্যই একটি পূর্ণাংগ একীভূত তত্ত্বে রূপদান করতে হবে, যা ব্যাখ্যা দেবে মহাবিশ্বের সব কিছুর। কিন্তু এরকম একটি একীভূত তত্ত্বের সন্ধানে নামলে একটি সঙ্কটের মুখে পড়তে হয়। ওপরে উল্লিখিত বিজ্ঞানের এই চিন্তা- ভাবনাগুলোতে ধরে নেওয়া হচ্ছে যে আমরা বুদ্ধিমান জীব, যারা স্বাধীনভাবে মহাবিশ্বকে দেখছি ও তা থেকে সিদ্ধান্ত নিচ্ছি। যদি এটা সঠিক হয়ে থাকে, তাহলে আমরা উন্নতি করতে করতে একদিন মহাবিশ্বের কার্যকরী নিয়মগুলোর কাছাকাছি পৌঁছতে পারব বলে মনে করা খুবই স্বাভাবিক।

অনুবাদকের নোটঃ
১। যেমন আইনস্টাইনের জেনারেল থিওরি অব রিলেটিভিটি বা সার্বিক আপেক্ষিক তত্ত্ব। ১০০ বছর আগে এর মহাকর্ষ তরঙ্গের পূর্বাভাস ২০১৬ এসে প্রমাণিত হয়। ফলে এটি ভালো তত্ত্ব হিসেবে আরো জোরালো স্বীকৃতি লাভ করে।
২। অধিবিদ্যা (Metaphysics) হল দর্শনের একটি শাখা। অন্য অনেক কিছুর মতো এরও জনক এরিস্টটল। বিশ্বের অস্তিত্ব, আমাদের অস্তিত্ব, সত্যের ধারণা, বস্তুর গুণাবলী, সময়, স্থান, সম্ভাবনা ইত্যাদি এর আলোচ্য বিষয়।
৩। অর্থ্যাৎ,তাদের মতে নির্দিষ্ট কোনো সূত্র প্রয়োগ করে মহাবিশ্ব সৃষ্টি করা হয়নি, তাই সেই আদি অবস্থার ব্যাখ্যা দেবার মত কোনো নির্দিষ্ট সূত্রের ব্যাখ্যা খোঁজা অনর্থক।
৪। মহাকর্ষ বল বস্তুদের দূরত্বের উপরও নির্ভরশীল- এটা ঠিক, কিন্তু দূরত্বতো আর বস্তুর নিজস্ব কোনো বৈশিষ্ট্য নয়।
৫। কারণ আমরাওতো মহাবিশ্বেরই একটি অংশ।

Category: articles

Read More...

একটি উদাহরণ চিন্তা করি। আমরা দেহের ওজোনের সাথে উচ্চতার সম্পর্ক দেখতে চাই। উচ্চতার উপর ওজোনের (ভর) প্রভাব কতটা সেটা জানতে চাই। ব্যাপারটার যৌক্তিকতা নিয়ে প্রশ্ন তোলা যেতেই পারে। আপাতত আমাদের উদ্দেশ্য রিগ্রেশন লাইন আঁকা বলে সে বিতর্ক তোলা থাকল।

তাহলে শুরুতেই আমরা গ্রাফের মাধ্যমে দুটো চলকের সম্পর্ক দেখব। ধরা যাক আমাদের কাছে নীচের ডেটা আছে।

আরও পড়ুন
R প্রোগ্রামিং: কীভাবে ইনস্টল ও ব্যবহার করবেন?

height = c(176, 154, 138, 196, 132, 176, 181, 169, 150, 175)
bodymass = c(82, 49, 53, 112, 47, 69, 77, 71, 62, 78) 

এবার এ দুটো নিয়ে একটি Scatter plot বা বিক্ষেপণ চিত্র আঁকা যাক।

plot(bodymass, height)

প্লটটিকে চাইলে আরেকটু স্টাইলিশ করে নেওয়া যায়। 

 plot(bodymass, height, pch=19, col="blue", xlab="Body Mass (kg)",
     ylab="Height (cm)", main="Bodymass vs Height")

এগুলোর মধ্যে কোন argument কেন ব্যবহার করা হল জানতে হেল্প সেকশন দেখতে পারেন। 

?plot

এবার আমরা কাঙ্খিত রিগ্রেশন লাইন আঁকব। আপাতত আমরা লিনিয়ার রিগ্রেশন লাইন নিয়ে কাজ করছি। 

আরও পড়ুন

লিনিয়ার ও নন-লিনিয়ার মডেলের পার্থক্য 

এক্ষেত্রে আমরা ব্যবহার করছি abline() ফাংশন। এ ফাংশনটি দিয়ে প্লটে অনুভূমিক (horizontal) বা উলম্ব (vertical) রেখা টানা হয়। যেমন উপরের প্লটে আমরা এভাবে বিভিন্ন রেখা টেনে বিন্দুগুলোর অবস্থান বুঝতে পারি। 

abline(h=155
abline(v=87))

এখানে h ও v বোঝাচ্ছে যে যথাক্রমে x ও y অক্ষের কোন পয়েন্ট দুটিতে রেখা আঁকা হবে। তবে ফাংশনটির প্রথম দুটি আর্গুমেন্ট হলো a ও b। এগুলো হলো রেখার যথাক্রমে ইন্টারসেপ্ট ও ঢাল। lm(height ~ bodymass) কমান্ডের মাধ্যমে আমরা এই a ও b এর মানই পাব। 

abline(lm(height ~ bodymass))

ব্যস রেখা হয়ে গেল। চাইলে এটাকে কাস্টোমাইজও করতে পারেন। কালার দিতে পারেন। 

আরও পড়ুন

প্লট কালারিং এর ৯ উপায়  

পুনশ্চ: 

যারা বুঝতে চান উপরের রিগ্রেশন রেখা কীভাবে এল। 

উপরের lm(height ~ bodymass) কমান্ড থেকে আমরা নীচের মডেলের মান পাব। 

$$Y=\alpha + \beta X + \epsilon$$

কমান্ডটির ফলাফল: 

Call:

lm(formula = height ~ bodymass)

Coefficients:

(Intercept)     bodymass

    98.0054       0.9528

এখানে $\alpha$ এর পরিমাপকৃত মান (a) 98.0054 আর $\beta$ এর মান (b) 0.9528। এরা হলো যথাক্রমে রিগ্রেশন লাইনের ইন্টারসেপ্ট বা x অক্ষ থেকে কর্তিত অংশ ও রেখার ঢাল। ঢাল মানে হলো x এক একক বাড়লে y কত একক বাড়ে। তার মানে আমাদের মডেলে ভর এক কেজি বাড়ালে উচ্চতা গড়ে ০.৯৫২৮ সেমি. বাড়ে। 

abline(lm(height ~ bodymass)) কমান্ডের মাধ্যমে এই দুটি মানই কাজে লেগেছে। উপরের প্লটের দিকে তাকালে খেয়াল করবেন, রেখাটিকে পেছন দিকে বাড়িয়ে দিলে বিন্দুতে গিয়ে 98.0054 বিন্দুতে গিয়ে x অক্ষকে ছেদ করবে। 

Category: articles

Read More...

রিগ্রেশন অ্যানালাইসিসের বড় একটি সমস্যা হলো লিনিয়ার ও নন-লিনিয়ার রিগ্রেশন মডেল আলাদা করে চিনতে পারা। সাধারণ ডেটা অ্যানালাইসিস বা মেশিন লার্নিং অ্যালগোরিদম প্রয়োগ করা-দুই ক্ষেত্রেই লিনিয়ার ও নন-লিনিয়ার মডেল চেনা খুব জরুরি।

বিষয়টি বলার আগে রিগ্রেশন (regression) আমরা কেন করি বা কী কাজে সে সম্পর্কে একটু বলে নেই।

একটি দৈব চলককে (random variable) আরেকটি চলকের মাধ্যমে প্রেডিক্ট বা অনুমান করার জন্য আমরা রিগ্রেশন মডেল ব্যবহার করি। রিগ্রেশনের মাধ্যমে প্রতিটি স্বাধীন (independent) চলক অধীন (dependent) চলককে কতটুকু প্রভাবিত করে সেটা জানা যায়। আর অধীন চলক সম্পর্কে অনুমানও করা হয় এই তথ্য কাজে লাগিয়েই।

যেমন ধরা যাক, আমরা জানতে চাই, মানুষের মাসিক আয় বাড়লে মাসিক খরচের কী অবস্থা হয়। অর্থাৎ কতটুকু আয় বাড়লে গড়ে কতটুকু খরচ বাড়ে। এবার ধরা যাক, দুটো চলকের সম্পর্ক তুলে ধরার জন্য আমরা একটি মডেল চিন্তা করলাম। যেটা এ রকম:
$$Y=\alpha + \beta X + \epsilon$$
এখানে Y হলো অধীন চলক। মানুষের আয়। আর X হলো স্বাধীন চলক। মাসিক খরচ। আর $\epsilon$ হলো ভ্রান্তি পদ (error term)। এই পদটি থাকার কারণ হলো আমরা আয় থেকে খরচ পুরোটা অনুমান করতে পারব না। অনুমান একটু এদিক-ওদিক হবে। $\epsilon$ এই "এদিক-ওদিক" বিষয়টিই দেখে। আর $\alpha$ ও $\beta$ নিয়ে একটু পরে বলছি।

এখানে আমাদের হাতে অনেকগুলো X ও Y এর মান থাকবে। যেমন ধরুন
\begin{array}{|c|c|}
\hline
X, & Y \\ \hline
৩০০০০ & ২৫০০০\\ \hline
৫০০০০ & ৪৩০০০ \\ \hline
১০০০০০ & ৮৬০০০\\ \hline
৫৫০০০ & ৪৯০০০ \\ \hline
৭৫৯০০ & ৬৭৫৫০\\ \hline
...& ...\\ \hline
\end{array}
এবার এই টেবিলের মানগুলো ব্যবহার করে আমরা উপরের মডেলের $\alpha$ ও $\beta$র মান পাব।  এখানে $\alpha$ ও $\beta$ হলো মডেলের প্যারামিটার (parameter)। $\alpha$ মানে হল X না থাকলে Y এর মান কত হবে। যেমন আমাদের মডেলে এর মানে হলো আয় না থাকলেও কত খরচ হবে। $\alpha$ এর মান সব সময় যৌক্তিক নাও হতে পারে।যেমন ধরুন X ও Y যদি হয় যথাক্রমে তুলা ও সুতার পরিমাণ, তাহলে $\alpha$ মানে হবে সুলা ছাড়াই কতটুকু সুতা পাওয়া যাবে। এই উদাহরণে এটার বাস্তব কোনো ভিত্তি নেই। তাই এক্ষেত্রে $\alpha$কে মডেল থেকে বাদ দিতে হবে।

আর $\beta$ মানে হলো X এক একক বাড়লে Y কতটুকু বাড়বে বা কমবে। যেমন উপরের মডেলে যদি আমরা $\beta$র মান পাই ০.২৫, তাহলে এর মানে হবে আয় ১ টাকা বাড়লে গড়ে খরচ বাড়বে ২৫ পয়সা।

এবার আজকের আলোচনার মূল বিষয়।
উপরে আমরা যে মডেলটা করলাম এটাকে বলে সিম্পল লিনিয়ার বা সরল রৈখিক রিগ্রেশন (simple linear)। কিন্তু এখানে X এর উপর যে-কোনো পাওয়ার থাকতে পারত। $\beta$ ও X এর সম্পর্কের রূপ হতে পারত কিম্ভুতকিমাকার।

তাহলে কীভাবে বুঝব কোন মডেলটা লিনিয়ার বা রৈখিক (linear) আর কোনটা নন-লিনিয়ার?

এখানে আরেকটি বিষয় মাথায় রাখতে হবে। রিগ্রেশনের ক্ষেত্রে মডেলকে লিনিয়ার বা নন-লিনিয়ার বলা হয় প্যারামিটারের সাপেক্ষে। গাণিতিকভাবে দেখলে নীচের সমীকরণটি নন-লিনিয়ার।
$$Y=\alpha + \beta X^2$$
কারণ X এর পাওয়ার এক (১) নয়। কিন্তু এই সমীকরণের সাথে $\epsilon$ যোগ করে রিগ্রেশন মডেল বানালে সেটি হবে লিনিয়ার মডেল।

তাহলে কখন নন-লিনিয়ার চিনব কীভাবে? 
তার জন্য আগে লিনিয়ার মডেল চিনতে হবে। একটি মডেল লিনিয়ার হবে যদি মডেলের প্রতিটি পদ হয় ধ্রুবক হয়, অথবা একটি প্যারামিটার ও একটি স্বাধীন চলকের (X) গুণফল হয়। আর সাথে ভ্রান্তি পদ তো থাকবেই। অতএব লিনিয়ার মডেলের সাধারণ রূপ হলো এ রকম:
$$Y=\alpha + \beta _1 X_1 + \beta _2 X_2 +\beta _k X_k + \epsilon \tag{1}$$
X এর পাওয়ার কম-বেশিও হতে পারে। কিন্তু প্যারামিটারের সাথে সম্পর্ক এই সমীকরণের মতো হলেই কেবল তাকে আমরা লিনিয়ার রিগ্রেশন বলব। এখন X এর জায়গায় যদি $X^2$ বা $X^3$ থাকে তাতেও লিনিয়ারই হবে। মানে নীচের মডেলও লিনিয়ার:
$$Y=\alpha + \beta _1 X_1 + \beta _2 {X_2}^2 + \epsilon$$
অনেকে আবার বলে থাকেন প্যারামিটারের ওপর পাওয়ার একের বেশি হলে নন-লিনিয়ার হবে। যেমন:
 $Y=\alpha + {\beta _1}^2 X_1 + \beta _2 {X_2}^2 + \epsilon$
কিন্তু এটি আসলে লিনিয়ার-ই। খেয়াল করে দেখুন $\beta$ এর উপর পাওয়ার হলেও পাওয়ার করে পাওয়া মান একটি ধ্রুবক-ই হবে। সেই ধ্রুবককে আমরা $\gamma$ বলতে পারি। ফলে সমীকরণ কিন্তু সেই "$X \times$" ধ্রুবক-ই হলো। ফলে এটিও লিনিয়ার-ই।

তার মানে লিনিয়ার রিগ্রেশনেও সরল রেখার বদলে কার্ভও পাওয়া যেতে পারে। নীচের ছবিতে শরীরের চর্বি ও বিএমআই (BMI = Body Mass Index) এর জন্য মডেল দেখানো হয়েছে। মডেল করা হয়েছে লিনিয়ার রিগ্রশন দিয়েই।

এ ছবিতে BMI ও চর্বির পরিমাণের সম্পর্কের নন-লিনিয়ার (অরৈখিক) রূপ দেখে মনে হতে পারে নন-লিনিয়ার রিগ্রেশন করতে হবে। আসলে এই অরৈখিক সম্পর্কের জন্যেও লিনিয়ার রিগ্রেশন যথেষ্ট। ছবির সোর্স: MiniTab ব্লগ। 

এবার তাহলে নন-লিনিয়ার মডেল কারা?
খুব সহজ। যে মডেলে উপরের ১ নং সমীকরণের মতো আকৃতি থাকবে না তারাই নন-লিনিয়ার। মানে লিনিয়ার মডেল মূলত এক রকম হলেও নন-লিনিয়ার মডেল নানা আকৃতিতে থাকতে পারে।

নিচে এমন কিছু উদাহরণ দেওয়া হলো।
$Y=\theta _1 \times X^{\theta _2} + \epsilon\\
Y=\theta _1 + (\theta _1 -\theta _2) \times e^{\theta _3 \times {\theta _4}}  + \epsilon\\
Y=\sqrt{\beta _1 + \beta _2 X} + \epsilon\\
Y=\sqrt{\beta _1 + \beta _2 X^2} + \epsilon
$

নন-লিনিয়ার রিগ্রেশনের এমন হাজারও উপায় থাকতে পারে। 

শেষ একটি বিষয়। উপরে আমরা দেখলাম, লিনিয়ার মডেলেরও কার্ভ থাকতে পারে। তাহলে কখন আমরা নন-লিনিয়ার মডেল ব্যবহার করব? এটা নিয়ে ভবিষ্যতে বিস্তারিত লিখব ইনশাআল্লাহ। আপাতত এই লেখাটি পড়তে পারেন। 

সূত্র
১। মিনিট্যাব ব্লগ
২। Johnson, J., Econometric Methods, 3rd Edition. 

Category: articles

Read More...

জিডিপি ও জিএনপি। দুটোই অর্থনীতির গুরুত্বপুর্ণ বিষয়। দুটোই একটি অর্থনীতিতে উৎপাদিত সবগুলো পণ্য ও সেবার (goods and services) বাজার মূল্য পরিমাপ করার চেষ্টা করে। তাহলে পার্থক্যটা কোথায়? পার্থক্যটা হলো ব্যাখ্যায়। 

জিডিপির পূর্ণ রূপ হলো Gross Domestic Product (GDP)। বাংলায় বলা হয় মোট অভ্যন্তরীণ উৎপাদন। একটু চিন্তা করলেই বোঝা যাবে অভ্যন্তরীণ শব্দটিই এখানে জিডিপির মূল ব্যাখ্যা। কোনো একটি দেশের সীমানার অভ্যন্তরে একটি নির্দিষ্ট সময়ে যে পণ্য ও সেবাগুলো তৈরি হবে, সেগুলোর মোট বাজার দরই হলো জিডিপি। দেশের অর্থনীতির শক্তি যাচাই করা হয় এর মাধ্যমেই। অনেক সময় বিনিয়োগকারীরা দেখেন, যে দেশে তারা বিনিয়োগ করতে যাচ্ছেন, তার জিডিপি যথেষ্ট ভালো কি না। নীতিমালা প্রণয়নের জন্যে সরকারকেও জিডিপি নিয়ে কাজ করতে হয়। 

তাহলে জিএনপি কী হতে পারে? অনেকের কাছে এটা ইতোমধ্যে স্পষ্ট হয়ে গেছে। অবশ্য এটা মনে হওয়াও অস্বাভাবিক নয় যে জিডিপির মতো দারুণ একটি পরিমাপ থাকতে অর্থনীতির শক্তি পরীক্ষার জন্য আর কিছুর কি প্রয়োজন হতে পারে?

আসলে এমন দেশ খুঁজে পাওয়া দুষ্কর যেখানে সব মানুষই নিজের দেশে থাকেন। দেশের অর্থনীতে তো সেইসব প্রবাসীদের অনেকও ভূমিকা রাখেন। কিন্তু জিডিপেতে সেই হিসেবটা আসেনি। সেই কাজটি করে জিএনপি বা Gross National Product (GNP)। বাংলায় বলে মোট বা স্থুল জাতীয় উৎপাদন। এটি হিসেব করে যে দেশের সকল মানুষ বা দেশীয় সকল প্রতিষ্ঠান পৃথিবীর যে কোন প্রান্তে বসেই মোট কী পরিমাণ উৎপাদন করল। যেমন ধরুন, বাংলাদেশি একটি প্রতিষ্ঠান কাজ করছে জার্মানিতে। তাহলে এটি যে পরিমাণ বাজারমূল্যের উৎপাদন করবে, সেটিও জিএনপিতে যোগ হবে। 

জিএনপি কি জিডিপির চেয়ে কম হতে পারে?

সাধারণত হয় না। তবে অনেক সময় হতেই পারে। যদিও ব্যাপারটাকে অসম্ভব মনে হচ্ছে। অসম্ভব মনে হবার কারণ হলো জিএনপিতে তো বেশি সংখ্যক মানুষ বা প্রতিষ্ঠানের উৎপাদনের হিসেব আসছে। কিন্তু একটু ভালো করে খেয়াল করলেই দেখা যাবে, জিডিপির সংজ্ঞায় ছিল দেশের সীমানা। আর জিএনপির সংজ্ঞায় আছে দেশীয় সব মানুষ বা প্রতিষ্ঠান। এ কারণে দেশের সীমানার ভেতরে থেকেও কিছু মানুষ বা প্রতিষ্ঠান জিএনপির হিসেবে আসবে না। কারণ সেই মানুষ বা প্রতিষ্ঠানগুলো ভিন্ন দেশীয়। ফলে তাদের উৎপাদনের হিসেব চলে যাচ্ছে ভিন্ন দেশের জিএনপিতে। 

জিডিপি বেশি হবে নাকি জিএনপি সেটা তাই নির্ভর করে দেশে বিদ্যমান দেশীয় ও বিদেশী প্রতিষ্ঠানের উৎপাদনের অনুপাতের উপর। 

চীনের কথাই ধরুন। পাব্লিক ডেটা প্ল্যাটফর্ম Knoema-এর হিসেব অনুসারে দেশটির জিডিপি জিনপির চেয়ে ৩০ হাজার কোটি ডলার বেশি। কারণ হলো দেশটিতে বিদেশি প্রতিষ্ঠানের কাজ অনেক বেশি। আবার ঠিক উল্টো কারণে যুক্তরাষ্ট্রের জিনপি জিডিপির চেয়ে ২৫ হাজার কোটি ডলার বেশি। 

জিডিপি ভালো না জিএনপি ভালো?

দুটি পরিমাপ প্রায় একই কাজ করলেও জিডিপির ব্যবহারই বেশি। সে তুলনায় জিএনপির ব্যবহার কম। তবে অর্থিনীতির সঠিক চিত্র তুলে ধরতে দুটোরই ব্যবহার হওয়া উচিত। 

এদিকে বিশ্ব ব্যাংক ও জাতিসংঘ আরেকটি পরিমাপ ব্যবহার করার প্রতি জোর দেয়। এটি তাদের মানব সূচকের (Human Development Index) ওপর ভিত্তি করে তৈরি। নাম জিএনআই বা মোট জাতীয় আয় (Gross National Income)। তবে জিডিপি ও জিএনপি উৎপাদন পরিমাপ করলেও নাম থেকেই বোঝা যাচ্ছে জিএনআই আসলে পরিমাপ করে ইনকাম বা আয়। 

সূত্রঃ

১। ইনভেস্টোপিডিয়া

২। উইকিপিডিয়া: Knoema 

Category: articles

Read More...

[লিখেছেনঃ ড. রহমতুল্লাহ ইমন] 

পরিসংখ্যানের সঠিক সংজ্ঞা নিয়ে নানা মুনির নানা মত রয়েছে। সন্দেহ নেই সবচে জনপ্রিয়তা পেয়েছে এটি উপাত্ত সংগ্রহ আর উপস্থাপনের বিষয় হিসেবে। তবে পরিসংখ্যানের এমন সংজ্ঞা কিন্তু খুবই সেকেলে। আজ থেকে হাজার পাঁচেক বছর আগেও কিন্তু মানুষ উপাত্ত সংগ্রহ করেছে, উপস্থাপন করেছে। অথচ আমরা বলছি পরিসংখ্যানের উৎপত্তি উনিশ শতকের শেষে। কী এমন হয়েছিল সে সময় যাতে আমরা তাকে পরিসংখ্যানের উদ্ভবের কাল বলতে পারি?

আসলে সে সময়ে সম্ভাবনা তত্ত্বকে কাজে লাগিয়ে বর্তমানের তথ্য উপাত্তের ওপর ভিত্তি করে ভবিষ্যৎ সম্পর্কে পূর্বাভাস দেয়া শুরু হয়েছিল। চেরনভ ও মোজেস যেমনটা ১৯৫৯ সালে বলেছেন,

 Statistics is the science of prediction and decision making in the face of uncertainty। 

আসলেও তাই। অনিশ্চয়তার মুখে সিদ্ধান্ত নিতে পারার ক্ষমতা যার আছে সে যে কালের বিচারে সবার থেকে এগিয়ে যাবে সেটাই তো স্বাভাবিক। কিন্তু কীভাবে আমরা অনিশ্চয়তার মুখে সিদ্ধান্ত নেই?

এ জগতে কোন কিছুই নিখুঁত নয়, আবার কোন কিছুই আমরা পুরোপুরি জানতেও পারি না। তারপরেও সত্য সন্ধানের প্রচেষ্টা তো থেমে থাকেনি কখনো। অজানাকে জানার, অচেনাকে চেনার প্রচেষ্টাই হল বিজ্ঞান। পরিসংখ্যানও বিজ্ঞান একারণেই। আমরাও অজানাকে জানার চেষ্টা করে থাকি। আমাদের অজানা হল সমগ্রকের (population) কোন বিশেষ বৈশিষ্ট যাকে আমরা পরামিতি (parameter) বলে থাকি। আর তা আমরা জানার চেষ্টা করে থাকি সংগৃহীত তথ্য উপাত্তের ভিত্তিতে।

তাহলে কী দাঁড়াল অবশেষে? পরিসংখ্যান হল জানার মাধ্যমে অজানাকে সন্ধান করার বিজ্ঞান। কী অবাক করা কথা? বিশ্বকবি রবীন্দ্রনাথ ঠাকুর ঠিক এই কথাটিই বলেছিলেন শতবর্ষ আগে। ১৯২৪ সালে তাঁর লেখা গান,

আকাশভরা সূর্য-তারা, বিশ্বভরা প্রাণ,
তাহারি মাঝখানে আমি পেয়েছি মোর স্থান,
বিস্ময়ে তাই জাগে আমার গান॥

এই গানটির মাঝেই তিনি উল্লেখ করেছেন সেই অমোঘ বাক্যটি

কান পেতেছি, চোখ মেলেছি, ধরার বুকে প্রাণ ঢেলেছি,
জানার মাঝে অজানারে করেছি সন্ধান,
বিস্ময়ে তাই জাগে আমার গান॥

আমার ক্ষুদ্র জ্ঞানে পরিসংখ্যানের এর চাইতে ব্যাপক ও নিখুঁত সংজ্ঞা আর কেউ কখনো দেননি।
ছোট্ট একটা উদাহরণ দেয়া যাক। আমার জানার ইচ্ছে হল রাজশাহী বিশ্ববিদ্যালয়ের ছাত্ররা সপ্তাহে গড়ে কতক্ষণ লাইব্রেরী ব্যবহার করে। এর একটি প্রকৃত মান নিশ্চয়ই আছে কিন্তু আমার সেটা জানা নেই। আমি দৈবচয়নের (random sampling) মাধ্যমে ১০ জন ছাত্রছাত্রীকে নির্বাচন করলাম। এবার তাদের জিজ্ঞাসা করলাম সপ্তাহে তারা কতক্ষণ লাইব্রেরি করে? তাদের কাছ থেকে পাওয়া উত্তরগুলো হল ঘন্টার হিসেবে ০, ১, ০, ৪, ০, ০, ৬, ৮, ৩, ০।

এই উপাত্তগুলো এখন আমার জানা। আর এই জানা মানগুলো দিয়েই আমি অজানা কে জানার চেষ্টা করব। যদিও আমি জানি না এর মান কত তবুও যুক্তির খাতিরে ধরে নিলাম তা ২। তাহলে আমি কি আমার জানা তথ্যগুলোকে এভাবে প্রকাশ করতে পারি না?
০ = ২ – ২
১ = ২ – ১
০ = ২ – ২
৪ = ২ + ২
০ = ২ – ২
০ = ২ – ২
৬ = ২ + ৪
৮ = ২ + ৬
৩ = ২ + ১
০ = ২ – ২

অর্থাৎ
জানা (উপাত্ত) = অজানা (প্রকৃত মান) + বিচ্যুতি

এখানে প্রকৃত অজানা মান ২, আর তা থেকে উপাত্তগুলো কখনো -২, -১, -২, +২, -২, -২, +৪, +৬, +১, -২ এভাবে বিচ্যুত হয়ে আছে। এখান থেকে আরও বোঝা যাচ্ছে যে বিচ্যুতি (error) যত কম হবে ততই উপাত্ত প্রকৃত অজানা মানের কাছকাছি পৌঁছাবে। সবচে ভাল হত যদি সবগুলো বিচ্যুতিই শূন্য হত যাতে প্রতিটি উপাত্তই হুবহু প্রকৃত মানের সমান হত। কিন্তু বৈচিত্রই তো এ জগতের প্রধান বৈশিষ্ট। স্রষ্টা কোন কিছুই তো একদম এক ছাঁচে সৃষ্টি করেননি। আমরা বড়জোর যা পারি তা হল এই বিচ্যুতিকে যথাসম্ভব কমিয়ে আনতে।

আমরা লিখতে পারি
বিচ্যুতি = উপাত্ত - প্রকৃত অজানা মান

আমরা এমনভাবে উপাত্ত থেকে প্রকৃত অজানা মান বের করব যাতে বিচ্যুতির বর্গ সমষ্টি (sum of square errors) হয় সর্বনিম্ন।

আমরা এখানে কেন বিচ্যুতির বর্গ নিলাম? গণিতের কলনবিদ্যার (calculus) অন্তরীকরণ (differentiation) থেকে আমরা জানি যে কোন ফাংশন ভা অপেক্ষককে (function) তার পরামিতির সাপেক্ষে অন্তরীকৃত করার পর সেখান থেকে পরামিতির এমন মান পাওয়া যাবে যা ঐ অপেক্ষককের বৃহত্তম বা ক্ষুদ্রতম মান নির্ণয় করতে পারবে। বিচ্যুতির চিহ্নমুক্ত সমষ্টি (sum of absolute errors) পরামিতি থেকে উপাত্তগুলোর দূরত্ব নির্দেশ করে বটে কিন্তু এই অপেক্ষকটিকে পরামিতির সাপেক্ষে অন্তরীকরণ করা যায় না।

তাই গাণিতিক সুবিধার কারণেই আমরা বিচ্যুতির বর্গসমষ্টিকে বেছে নিয়েছি। এর অর্থ কিন্তু আবার এও নয় যে বিচ্যুতির চিহ্নমুক্ত সমষ্টির সর্বনিম্ন মান বের করা যায় না। এটা যায়, তবে অন্তরীকরণের মাধ্যমে নয়- তুলনামূলকভাবে অনেক বেশি জটিল পদ্ধতির মাধ্যমে। আর সেকারণেই এটা জনপ্রিয় হয়ে উঠতে পারেনি।

অপেক্ষকটিকে অন্তরীকরণের পর এখান থেকে যে সমাধান আসে তা খুবই চিত্তাকর্ষক। পরামিতির নিরূপকটি (estimate) আসলে নমুনা গড় (sample mean)। আমরা আগেই বলেছি যে পরামিতির নিরূপকটি ঐ অপেক্ষককের বৃহত্তম বা ক্ষুদ্রতম মান নির্ণয় করতে পারে। নমুনা গড় আসলে কী দেবে সেটা পরীক্ষার জন্য আমরা অপেক্ষকটিকে তার পরামিতির সাপেক্ষে আরেক দফা অন্তরীকৃত করব। শাস্ত্র বলছে অপেক্ষকটির দ্বিতীয় দফা অন্তরীকৃত মান ধণাত্মক হলে অপেক্ষকটি ক্ষুদ্রতম মান দেবে আর অন্তরীকৃত মান ঋণাত্মক হলে অপেক্ষকটির মান হবে বৃহত্তম।

বিচ্যুতির বর্গসমষ্টিকে দ্বিতীয় দফা অন্তরীকরণ করার পর যেহেতু এর মান পাওয়া যায় ২, সেহেতু একথা নির্দ্বিধায় বলা চলে যে নমুনা গড় জানা অজানার পার্থক্যের দূরত্বকে সবচে কমিয়ে আনবে। আর সে কারণেই নমুনা গড় হবে প্রকৃত মানের সবচাইতে গ্রহণযোগ্য অনুমিত মান।
এই উদাহরণের উপাত্ত থেকে পাওয়া নমুনা গড় হল ২.২ ঘন্টা। তাই ছাত্রছাত্রীদের লাইব্রেরীতে কাটানোর প্রকৃত সময় যদি সত্যি সপ্তাহে ২ ঘন্টা হয় তবে অনুমিত মান তার বেশ কাছাকাছি। তবে এই কাছাকাছি ব্যাপারটা তাৎপর্যপূর্ণ কিনা সেটাও পরীক্ষা করার পদ্ধতি আছে। আর এক্ষেত্রে নমুনা সংখ্যা যেহেতু কম আমরা বেছে নেব স্টুডেন্টের t নিবেশনকেই।

আর এভাবেই বারে বারে জানার মাঝে অজানাকে খুঁজে নেয় পরিসংখ্যান।
জয়তু রবীন্দ্রনাথ!

লেখক: অধ্যাপক, ম্যাথেম্যাটিক্যাল সায়েন্সেস,  Ball State University। 

Category: articles

Read More...

R-এ অধিকাংশ কাজই একাধিক উপায়ে করা যায়। নান্দনিক গ্রাফিক্সের জন্য কালার বড় ভূমিকা পালন করে। R-এ প্লট কালার করা যায় অন্তত ৯ উপায়ে। চলুন জেনে নেওয়া যাক সে উপায়গুলো।

ও, আচ্ছা। প্লট করার জন্যে তো হাতে কিছু ডেটা লাগবে। আগে ডেটা বানিয়ে নিই তাহলে।

x=rexp(1000)
y=(rnorm(1000)

আর R এর ডিফল্ট ফন্ট আমার পছন্দ না। তাই ফন্টটা একটু পালটে নিচ্ছি। এটা অপশনাল। না করলেও দুনিয়া ধ্বংস হয়ে যাবে না।

par(family="serif")

তাহলে এবার আসল কাজে আসা যাক! মনে রাখতে হবে R-এ কমেন্ট শুরু হয় # চিহ্ন দিয়ে। মানে # চিহ্নের পরের কোড রান হবে না। 

১। কালার সিকুয়েন্স 

plot(x, y, col=4, pch=16, cex=1.4, main="Scatter Plot",
     xlab="X values", ylab="Y values")
grid() # optional

এখানে plot ফাংশনের col ছাড়া বাকি আর্গুমেন্টগুলো অপশনাল। প্লটের নান্দনিকতার স্বার্থেই যোগ করা। যাই হোক, এখানে খেয়াল করুন, আমরা শুধু একটি সংখ্যা বসিয়ে দিয়েছি। R-এ প্রায় প্রতিটি সংখ্যার বিপরীতে একটি করে কালার আছে। আপনি চাইলে এখানে 4,5,10, 25, 36- যাই ইচ্ছে বসিয়ে দেখতে পারেন। 

আবার কখনও একই সাথে অনেকগুলো কালারের প্রয়োজন হলে col=1:10 বা c(1,2,4,6,7,3) ফরম্যাটেও লিখতে পারেন। চেক করেই দেখুন না!

আবারও মনে করিয়ে দেই। উপরের grid কমান্ডটি কিন্তু অপশনাল। এটা আসলে প্লটে বক্স আঁকে। # দিয়ে অপশনাল কথাটা বলা আছে।

২। কালার নেইম 

এক্ষেত্রে আমরা সরাসরি কালারের ইংরেজি (সাধারণত) নাম বসিয়ে দেব।

plot(x, y, col="blue", pch=16, cex=1.4, main="Scatter Plot",
     xlab="X values", ylab="Y values")

একই প্লট পাওয়া গেল। এখানেও চাইলে আপনি একাধিক কালার ব্যবহার করতে পারেন একই প্লটে। Scatter প্লটের ক্ষেত্রে একাধিক কালার আপাতত দরকার না হলেও হিস্টোগ্রামে দরকার হতে পারে। যেমনঃ

hist(x, col=c("blue", "grey"))
box() #optional
grid() #optional

এক্ষেত্রে যেটা দরকার, তা হলো সবগুলো কালারের নাম জানা। সেটাও সহজ। প্রথমত, এই লিঙ্ক থেকে R-এর সবগুলো কালার নেইম পাবেন। অফলাইনে ব্যবহার করতে ডাউনলোড করে নিতে পারেন। আরও সহজে নামগুলো দেখতে চাইলে colors() কোড ব্যবহার করুন। তবে এক্ষেত্রে কোন কালারের চেহারা কেমন সেটা বোঝা যাবে না। সেটা বোঝা যাবে পিডিএফ ফাইলটা থেকে (লিঙ্কের)।

৩। অটো কালার ১ (topo.colors(10))

hist(y, col=topo.colors(10))
grid() #optional
box() #optional

যতটা আলাদা কালার চাই, ব্র্যাকেটের ভেতরে সেটা উল্লেখ করে দিতে হবে। 

৪। অটো কালার ২

hist(x, col=heat.colors(12))
grid() #optional
box() #optional

এক্ষেত্রেও যতটা আলাদা কালার চাই, ব্র্যাকেটের ভেতরে সেটা উল্লেখ করে দিতে হবে। 

৫। অটো কালার ৩

hist(x, col=terrain.colors(3))
grid() #optional
box()#optional

এক্ষেত্রেও যতটা আলাদা কালার চাই, ব্র্যাকেটের ভেতরে সেটা উল্লেখ করে দিতে হবে। 

৬। হেক্সাডেসিমাল কোড

এই সাইট ভিজিট করুন। অথবা hexadecimal colors লিখে সার্চ দিলে আরও নানান সাইট পাওয়া যাবে। এখান থেকে হেক্সাডেসিমাল কোডটি বা কোডগুলো বসিয়ে দিতে পারেন। 

hist(x, col="#80ff00")
grid() #optional
box()#optional

৭,৮। Rgb ও hsl কালার কোড

উপরে দেওয়া লিঙ্কেই বাকি দুটি কালার কোডও পাবেন। এ দুটোতে সামান্য জটিলতা আছে। লিঙ্কে যেভাবে আছে ঠিক সেভাবে দিলে হবে না। rgb() ফাংশনের ভেতরে ৩টি সংখ্যা দিতে হবে। rgb মানে আসলে রেড, গ্রিন ও ব্লু। অতএব, ভেতরে যথাক্রমে লাল, সবুজ ও নীলের অনুপাত বসাতে হবে। প্রতিটি সংখ্যা হবে ০ থেকে ১ এর মধ্যে। ০ ও ১ দেওয়া যাবে। 

hist(x, col=rgb(0,0.8,0.9))
grid() #optional
box()#optional

আর hsl কোডে আরেকটু জটিলতা আছে। এটাকে ব্যবহার করতে চাইলে এই টিউটোরিয়াল পড়ুন। 

৯। সেরা কৌশল 

এতক্ষণ যেগুলো বললাম এগুলোর অনেকগুলো থেকেই অনেক সময় সেরা কম্বিনেশন বাছাই করা কঠিন। যেমন নীচের ম্যাপটি আঁকতে চাই। ম্যাপটি আঁকার বিস্তারিত কোড আছে এখানে। 

spplot(zilla, "literacy",col.regions=terrain.colors(5),
       cuts=4, col='transparent', main='Sample Map',
       scales=list(draw=T))

এখানে terrain.colors(5) ভালো কাজ করেছে। তবে কালারের সিকুয়েন্স ধরে রাখতে পারেনি। 

কিন্তু এটায় দেখুন, মান বাড়ার সাথে কালার গাঢ় হয়েছে। অথবা নীচের হিস্টোগ্রাম দেখুনঃ

নানান ক্ষেত্রেই এটার প্রয়োজন অনুভব করবেন। এক্ষেত্রে একটি প্যাকেজ লাগবে। নাম RColorBrewer। ইন্সটল করে লোড করে নিন। 

install.packages("RColorBrewer")
library(RColorBrewer)

এবার আবার হিস্টোগ্রাম আঁকি। 

hist(x, col=brewer.pal(n=5, name='YlGn'), ylim=c(0,500))

এখানে n এর জায়গায় যতগুলো কালার চান সেটা বসাবেন। আর name এর জায়গায় কী বসাবেন সেটার উপরই বির্ভর করছে কালার কেমন হবে। নীচের ছবিতে দেখে নিন কোডগুলো। বড় করে দেখতে এখানে ক্লিক করুন। 

 

আপনাকে আর পায় কে। দৃষ্টিনন্দন প্লট এঁকে তাক লাগিয়ে দিন বসকে!

এর বাইরে আপনি আরও কিছু জানলে কমেন্টে অবশ্যই জানাবেন।

Category: articles

Read More...

ইংরেজি উইকিপিডিয়ার বাংলাদেশ পেইজের এজুকেশন সেকশনে শোভা পাচ্ছে আমার আঁকা এই ম্যাপটি। ম্যাপটিতে বাংলাদেশের বিভিন্ন এলাকার স্বাক্ষরতার চিত্র তুলে ধরা হয়েছে। এমন একটি ম্যাপ R-এ আঁকা অকল্পনীয় রকম সহজ। এটা নিয়েই আজকের পোস্ট।

প্রথম কাজ ম্যাপ আকাঁর জন্য প্রয়োজনীয় শেইপ ফাইল (shape file)। R এর plot ফাংশন দিয়ে শুরুতে আমরা এই ফাইলের একটি অংশই প্লট করব। বাংলাদেশের জন্য বানানো শেইপ ফাইলটি আপনাকে ডাউনলোড করে নিতে হবে। এটা পাওয়া যাবে এই লিঙ্কে। লিঙ্ক থেকে Shapefile টি ডাউনলোড করে নিন।

☛ এখানে ক্লিক করেও ডাউনলোড করতে পারেন।

একটি জিপ ফাইল ডাউনলোড হবে। ফাইলটাকে আনজিপ করে নিন। আনজিপ করে এমন একটি ফোল্ডার পাবেন।

এই ফোল্ডারে আসলে বিভিন্ন আলাদা আলাদা ম্যাপ আঁকার ফাইল আছে। যেমন আলাদা করে বিভাগের ম্যাপ আঁকতে চাইলে দরকার হবে BGD_adm1 ফাইলটি। জেলাগুলোও দেখাতে চাইলে BGD_adm2 ফাইলটি। আর উপেজেলাগুলোও আলাদা করে দেখাতে চাইলে লাগবে BGD_adm3 ফাইলটি।

☛ লক্ষ্য করুন 
ভার্সনভেদে ডাউনলোড করে আনজিপ করা ফাইলের নাম আলাদা হতে পারে। যেমন একটি ক্ষেত্রে এটির নাম gadm36_BGD_2। 

একটি বিষয় বুঝে নেওয়া ভাল। Shapefile আসলে অনেকগুলো আলাদা ফাইলের সমন্বয়। যেমন, BGD_adm1 নামে অনেকগুলো ফাইল আছে। একই নামের সবগুলো ফাইল একই ফোল্ডারে থাকলে তবেই কেবল ফাইলটি কাজ করবে। তার মানে এই নয় যে ঐ ফোল্ডারে অন্য ফাইল থাকা যাবে না। আমাদের এই ফোল্ডারেই কিন্তু চারটি ম্যাপ আঁকার ফাইল আছে।

এবার ম্যাপটিকে R-এ পড়াতে হবে। এজন্য "rgdal" নামে একটি প্যাকেজ লাগবে। R এর প্যাকেজ ইনস্টল করার মতো সহজ কাজ দুনিয়াতে আর নেই। ইনস্টল ও লোড করে নিন।

☛ টিপস: Rstudio ব্যবহার করলে কাজটি সহজ হবে। না থাকলে ইনস্টল করে নিন। শুধু ম্যাপিং-ই না, R এর করা কাজগুলো হাজারো উপায়ে সহজতর হয়ে যাবে। Rstudio তে কোড run করতে Ctrl+Enter চাপুন।

install.packages("rgdal")
library(rgdal)

এবার Shapefile টিকে লোড করার পালা।

zilla=readOGR("D:/R/RGIS/BD", layer="BGD_adm2")

খেয়াল করুন, এখানে "D:/R/RGIS/BD" হলো BGD_adm2 ফাইলটি যে ফোল্ডারে আছে তার লোকেশন। আপনি ফাইলগুলো যেখানে রাখবেন সেই ফোল্ডারের লোকেশন এখানে লিখতে হবে। আর layer অংশটিতে কিছু করা লাগবে না। অবশ্য আপনি যদি উপজেলার ম্যাপ আঁকতে চান, তাহলে BGD_adm3 লিখতে পারেন।

☛ layer এর জায়গায় ফোল্ডারের ফাইল থেকে সঠিক নামটি বসাতে হবে।

এবার "zilla" অবজেক্টটি প্লট করে দেখুন। বাংলাদেশের ম্যাপ পেয়ে যাবেন।

plot(zilla, col="green")

কিন্তু আমরা তো শুধু এটা চাই না। আমরা চাই, অন্য একটু ক্রাইটেরিয়ার ভিত্তিতে আলাদা আলাদা জেলায় আলাদা আলাদা কালারিং হবে। তাহলে প্রতিটা জেলার সেই তথ্যটা লাগবে। আমরা আপাতত চাই বাংলাদেশের স্বাক্ষরতার হারের ভিত্তিতে রং-এর তারতম্য। এই কাজটি করার জন্য আমাদের sp প্যাকেজটি লাগবে। 

install.packages("sp")
library(sp)

বাংলাদেশের প্রতিটি জেলার স্বাক্ষরতার হার আমাদেরকে zilla অবজেক্টটিতে যোগ করতে হবে। তার আগে ৬৪টি জেলার তথ্য zilla অবজেক্টে-এর সাথে মিলিয়ে সাজিয়ে নিতে হবে। এখানেই Rstudio না থাকলে একটু সমস্যা হবে। zilla অবজেক্টে জেলাগুলোর ক্রম দেখার জন্য Rstudioতে View(zilla) কোড রান করলে ID_2 ও NAME_2 কলামে যথাক্রমে জেলার ক্রম ও নাম দেখা যাবে। এই ক্রম অনুসারেই আপনাকে স্বাক্ষরতার তথ্য লিপিবদ্ধ করতে হবে। 

কাজটি আপনি অনেকভাবে করতে পারেন। ৬৪টি জেলার হার একটি এক্সেল ফাইলে বসিয়ে ফাইলটিকে .csv আকারে সেইভ করে নিতে পারেন। আবার এক্সেল ফাইল সরাসরি পড়াতেও পারেন। এক্ষেত্রে readxl প্যাকেজ ব্যবহার করতে পারেন। আবার চাইলে সরাসরি R এর মধ্যেই হারগুলো নিয়ে একটি ভেক্টর বানিয়ে নিতে পারেন। যেমনঃ

literacy=c(61.24, 43.24,...) 

আপাতত আমরা csv ফাইল বানিয়ে রেখেছি। এটাই Rকে দিয়ে পড়াচ্ছি। এখান থেকে ডাউনলোড করে নিন। 

literacy=read.csv("D:/R/RGIS/literacy.csv")

"D:/R/RGIS/literacy.csv" অংশটিতে ফাইলটি যে ফোল্ডারে রেখেছেন তার পূর্ণ লোকেশন লিখতে হবে। 

এবার এটাকে আমরা zilla-এর সাথে যুক্ত করব। zilla অবজেক্টি ডেটা ফ্রেইম না হলেও ডেটা ফ্রেইমের কিছু নিয়ম এখানে খাটে। সেই কৌশলই আমরা কাজে লাগাব। 

zilla$literacy=literacy

Rstudio-তে View(zilla) রান করলে একেবারে ডান পাশের কলামে literacy দেখা যাবে। 

এবার আমরা প্রায় প্রস্তুত। তাহলে ম্যাপটা এঁকেই ফেলি! 

spplot(zilla, "literacy",col.regions=topo.colors(5),
       cuts=4, col='transparent', main='Sample Map',
       scales=list(draw=T))

বাহ! এইমাত্র আপনি সফল একজন ম্যাপ আর্টিস্ট হয়ে গেলেন। পাওয়া গেল ম্যাপটি।

এই কোডটির ব্যাখ্যা

Shapefile টিকে রাখতে হবে একদম শুরুতে (আমরা এখানে যাকে zilla নামে সেইভ করেছি)। তারপরেই যে কলামের তথ্যের ভিত্তিতে প্লট করতে চাই তার নাম (যেমন আমাদের এখানে literacy)। col.regions= অংশে হবে কালারগুলোর নাম। R প্রোগ্রামিং-এ কালার বসানোর অনেক উপায় আছে। topo.colors(5) হলো এমন একটি উপায়। যেখানে ৫টি কালার সেট হয়ে যাবে। আপনি চাইলে c("red", "green", ...) এভাবেও বসাতে পারেন। আবার heat.colors(5) বা terrain.colors(5) বসিয়েও দেখতে পারেন।

আরও পড়ুন 
☛ R প্রোগ্রামিং: প্লট কালারিং এর ৯ উপায়

col.regions অংশে যতগুলো আলাদা কালার বসিয়েছেন cuts অংশে তার ১ কম সংখ্যা বসবে। আপাতত এটা জানাই যথেষ্ট। আরও জানতে হলে ?spplot রান করে জেনে নিতে পারেন। 

Category: articles

Read More...

R এর গ্রাফগুলোতে এমনিতে গ্রিড থাকে না। কিন্তু চাইলে করা যাবে না, এমন কিছু R-এ খুঁজে পাওয়া দুষ্কর। আমরা আজকে নীচের গ্রাফটি আঁকার উপায় দেখব।

বরাবরের মতোই আগে লাগবে ডেটা। তো কিছু ডেটা বানিয়ে নেই। 

x=sample(30)+1:30
y=sample(30)+30:1
df=data.frame(x,y)
df.ts=ts(df,start=1980)

একটি টাইম সিরিজ ফরম্যাট বানিয়ে নিলাম। এবার চাইলে প্লটের ব্যাকগ্রাউন্ড সেট করে নিতে পারি। না করলেও দুনিয়া ধ্বংস হয়ে যাবে না। আপনার ইচ্ছা! 

par(bg="#8FBC8F")

এখানে #8FBC8F হলো হেক্স কোডে লেখা কালার। আপনি এ সাইট থেকে আরও নানান ধরনের কালার বসাতে পারেন। চাইলে আপনি red, blue ইত্যাদিও দিতে পারেন। 

x ও y চলকে বসানোর জন্য দুই রকম কালার ঠিক করে রাখি। 

color= c("red","yellow")

এবার প্রাথমিক প্লটখানা এঁকে ফেলি। এতে কিন্তু কোনো গ্রিড নেই। 

ts.plot(df.ts, gpars=list(col=color), lwd=5,
        ylab="Value", xlab="Year", main="Grid on R plot")

এবারই আমাদের মূল কাজ। মানে গ্রিড। 

grid(7,7, col="black", lwd=3, lty='solid')

7, 7 বোঝাচ্ছে যে x ও y অক্ষ বরাবর যথাক্রমে কয়টি করে লাইন আঁকা হবে। লাইনের রঙ, লাইনের প্রস্থ সবই চেঞ্জ করতে পারবেন ইচ্ছা মতো। 

আরও নানান উপায় দেখতে হেল্প ফাইল দেখে নিন। 

?grid

এবার প্লটে লিজেন্ড দিয়ে বুঝিয়ে দেওয়া যাক কোন লাইনটা কোন চলকের। 

legend("top", legend=names(df), ncol=2, col=color, pch=19)

তবে সবচেয়ে ভালো grid() ফাংশনের ভেতরে কিছুই না লিখলে। এতে করে y অক্ষের সাথে দাগগুলো নিজে নিজেই মিলে যাবে। দেখতে ও বুঝতেও হবে সহজ। অবশ্য প্লট ব্যাকগ্রাউন্ড সেট করলে কালার ম্যাচিং না হলে কালার যুক্ত করা যেতে পারে।

par(bg="#00bfff")
plot(sample(10,6), pch=19, col="white", type="b", lwd=2,
     ylab="Value")
grid()

এটায় কালার মিলছে না। তাই গ্রিডের কালার দিয়ে দিলাম।

par(bg="#00bfff")
plot(sample(10,6), pch=19, col="white", type="b", lwd=2,
     ylab="Value")
grid(col="black")

R প্লটে অটো গ্রিড 

এখানে আমরা প্লট করার জন্য ১০টি ভ্যালু থেকে ৬টি ভ্যালু স্যাম্পল নিয়েছি। তাই একই কোড রান করলেও গ্রাফটি এটা থেকে আলাদা আসার সম্ভাবনাই বেশি।

আরও পড়ুন 
☛  স্মুথ প্লট আঁকবেন কীভাবে 

Category: articles

Read More...

আমরা নীচের ছবির মতো একটি গ্রাফ আঁকতে চাই। যেখানে একই গ্রাফে অনেকগুলো টাইম সিরিজ ডেটা থাকবে।

একই গ্রাফে অনেকগুলো টাইম সিরিজ 

তো প্রথমেই আঁকার জন্যে আমাদের কাছে কিছু ডেটা থাকতে হবে। আপাতত আমরা নিজেরাই কিছু ডেটা বানিয়ে নিচ্ছি। আপনি চাইলেই এক্সেল বা CSV (কমা সেপারেটেড ভ্যালু) ফাইল থেকেও ডেটা লোড করতে পারেন।

x=seq(30000,40000,500)+rnorm(mean=500, sd=1000,n=21)
y=seq(29000,39000,500)+rnorm(mean=500, sd=1000,n=21)
z=x-y
df=data.frame(income=x, expense=y, balance=z)

এখানে আমরা df নামে একটি ডেটা ফ্রেইম তৈরি করলাম। আপনি চাইলে head(df) লিখে ডেটা ফ্রেইমের চলকগুলোর প্রথম ৬টি করে মান দেখে নিতে পারেন। এবার আমাদেরকে এই ডেটাকে টাইম সিরিজ ফরম্যাটে রূপ দিতে হবে। একটি চলক (variable) নিয়ে প্লট করার উপায়টা আগে একটু দেখে নেই। 

x.ts=ts(x, end=2018)

ts ফাংশন x চলকটিকে টাইম সিরিজ ফরম্যাটে রুপান্তর করল।  ?ts কমান্ডের সাহায্যে আপনি ts ফাংশনের আরও নানান অপশন দেখে নিতে পারেন। যেমন ডেটা কোন বছর শুরু হল, সেটা জানা থাকলে start=year অপশন ব্যবহার করতে পারেন। 

এবার আমরা একে প্লট করব

plot(x.ts) 

এটা খুব একটা সুন্দর হবে না। তার চেয়ে আরও কিছু attribute যোগ করলে ভাল হয়। 

plot(x.ts, col=3, lwd=2, ylab="Amount")

lwd এর কাজ হলো লাইন কতটা মোটা বা চিকন হবে তা ঠিক করা। lwd=1 দিলে সবচেয়ে চিকন হবে। আরও ভাল করতে চাইলে একটা ব্যাকগ্রাউন্ড যোগ করতে পারেন।

par(bg="gray")
plot(x.ts, col="red", lwd=2) 

একটি চলকের টাইম সিরিজ গ্রাফ 

এবার আমরা একই গ্রাফে আমাদের df ডেটাফ্রেইমের ৩টা চলক একত্রে আঁকবো। তাহলে একে আগে টাইম সিরিজ ফরম্যাট করা যাক। চেঞ্জ করে নতুন নাম দিলাম df.ts।

df.ts=ts(df, end=2018)

এবার একে প্লট করে ফেলি।

ts.plot(df.ts, gpars=list(col=topo.colors(3)), lwd=2,
        ylab="Amount")

খেয়াল করুন, এখানে আমরা plot ফাংশনের বদলে ts.plot ব্যবহার করলাম। 

topo.colors এর কাজ হলো অটোম্যাটিক কালার করে নেওয়া। ভেতরে ৩ মানে ৩টি কালার হবে। যেহেতু আমাদের চলক ৩টি। অটো কালার করার আরও অনেক উপায় আছে। যেমন terrain.colors(3), rainbow(3), heat.colors(3)। আবার ম্যানুয়ালিও কালার করা যাবে। 

ts.plot(df.ts, gpars=list(col=c("green",'Blue','Yellow'), lwd=2))। 

এবার legend দিয়ে বোঝাতে হবে কোন কালারের কী মানে। 

legend("topleft", legend=names(df), fill=terrain.colors(3), ncol=3)

ts.plot কমান্ডে col অপশনে যেটা থাকবে এখানে fill এর জায়গায় সেটাই দিতে হবে। ncol মানে লিজেন্ড বক্স এর কলাম কয়টি হবে। প্লট দেখে সুবিধামতো লিজেন্ড এর পজিশন ঠিক করতে হবে। topleft এর বদলে top, bottom, right, left বা এদের যে কোন রকম কম্বিনেশন ব্যাবহার করা যাবে। 

legend এর ভেতরের legend এর মানে হলো কালারগুলোর নাম কী কী হবে। ওপরের কোডে আমরা সরাসরি ডেটাফ্রেইমের কলাম নেইম দিয়ে দিয়েছি। চাইলে ইচ্ছামতো অন্য কিছুও দেওয়া যায়। 

legend("topleft", legend=c("red","green","yellow"), fill=terrain.colors(3), ncol=3)

আরেকটি অপশনাল কাজ বাকি। প্লটের ব্যাকগ্রাউন্ড একটু চেঞ্জ করে নিলে আরেকটু দৃষ্টিনন্দন হতে পারে। এটা আমাদের মোটামুটি ফাইনাল কাজ। 

par(bg="gray")
ts.plot(df.ts, gpars=list(col=topo.colors(3)), lwd=5, ylab="Amount", xlab="Year")
legend("topleft", legend=names(df), fill=topo.colors(3), ncol=3,)

এই প্লটটা স্বাভাবিকের মতো এবড়োথেবড়ো নয়। 

পড়ে নিন তাহলে 

☛ কীভাবে মসৃণ প্লট আঁকবেন?

Category: articles

Read More...

শুধু যে ডেটা অ্যানালিটিক্সের সিরিয়াস কাজেই R কারিশমা দেখায় এমন না। হাসতে-খেলতে মনের খোরাক যোগানোরও নানান উপাদান পাওয়া যাবে এর মধ্যে।

ggplot2 প্যাকেজ দারুণ সব ডিজাইন আঁকা যায়। তবে প্যাকেজের ভেতরে না গিয়েও বেশ দারুণ প্লট তৈরি করা যায়। যেমন, কোনো প্যাকেজ ছাড়াই আমরা এটা আঁকতে পারি।

এর কোড খুবই সরল। ভবিষ্যতে আমরা এর খুঁটিনাটি ব্যাখ্যা করব ইনশাআল্লাহ।

angle <- pi*(3-sqrt(5)) n <- 1000 t <- angle*(1:n) x <- sin(t) y <- cos(t) plot(x*t,y*t, pch=16, col="blue")

R এর অন্যতম বিখ্যাত প্যাকেজ হলো ggplot2। এর মাধ্যমেই আমরা নীচের ফুলটি এঁকে ফেলতে পারি।

R প্রোগ্রামিং দিয়ে আঁকা ফুল 

এর জন্যে প্রথমেই ggplot2 প্যাকজেটি লোড করতে হবে।

library(ggplot2)

আর যদি প্যাকেজটি আগে ইনস্টল করা না থাকে তবে ইনস্টল তো করে নিতেই হবে।

install.packages("ggplot2")

ফুলের আকার-আকৃতির জন্যে প্রথমে কিছু ফর্মুলা লিখে নিতে হচ্ছে। এরপরেই পাওয়া যাবে কাঙ্খিত সেই বাহারি ফুল!

angle=pi*(3-sqrt(5))
n=500
t=angle*(1:n)
x=sin(t)
y=cos(t)
df=data.frame(t,x,y)
library(ggplot2)
p=ggplot(df, aes(x*t,y*t))
p+geom_point(size=8, alpha=0.6, color='blue')+
theme(title=element_blank(),
text=element_blank(),
panel.grid = element_blank(),
panel.background = element_rect(fill='white'))

চাইলেই আপনি আরও হাজার রকম ফুল আঁকতে পারেন। শুধু ওপরের angle টাই পাল্টে দেখুন না! যেমন এইটুকু শুধু পাল্টালাম। ফলাফল নিজেই দেখুন।

angle=pi*(5-sqrt(10))
n=700

আবার এই কোড কী করল দেখুন!

angle=2.73*(3-sqrt(4))
n=300

R প্রোগ্রামিং দিয়ে আঁকা ফুল

Category: articles

Read More...

সকল কাজের মোক্ষম কাজী R প্রোগ্রামিং ল্যাঙ্গুয়েজ। ইমেইল করার জন্যেও এতে রয়েছে দারুণ একটি প্যাকেজ। নাম: mailR।

শুরুতে আপনাকে R এর প্যাকেজটি ইনস্টল ও লোড করে নিতে হবে।

install.packages("mailR")

এই প্যাকজেটি আবার R এর আরেকটি প্যাকেজ rjava এর ওপর নির্ভর করে। তবে সেটা আপনাকে আলাদা করে ইনস্টল করা লাগবে না। R নিজেই করে নিবে। তবে আপনার পিসিতে জাভা ইনস্টল করা থাকতে হবে। না থাকলে এখান থেকে ডাউনলোড করে ইনস্টল করে নিন। এটা একবারই করতে হবে।
আপনার কম্পিউটার 64 bit হলে জাভার ৬৪ বিটের ভার্সন নিবেন কিন্তু।

এবার library(mailR) কোড রান করে প্যাকেজটি লোড করুন।
এবার নীচের কোডখানা নিজের মতো করে সাজিয়ে পাঠিয়ে ফেলুন আপনার ইমেইল।

send.mail(from="yourmail@mail.com",
to="sendto@mail.com",
subject="R Email",
body="Write what you want to send",
html=T,
smtp=list(host.name = "smtp.gmail.com",
port = 465,
user.name = "yourmail@mail.com",
passwd = "password",
ssl = T),
authenticate=T,
attach.files="C:\\file_path")

এখানে নিজের মতো করে সব কিছু ঠিক করে দিয়ে কোডটি রান করালেই কেল্লা ফতে!

☛ ফাইল অ্যাটাচ করতে হলে attach.files অংশে ফাইলের লোকেশন লিখতে হবে।

☛ গুগোলের জিমেইল থেকে ইমেইল পাঠাতে গেলে সরাসরি কাজ করবে না। সেক্ষেত্রে গুগোল আপনাকে একটি ইমেইল পাঠিয়ে বাইরের অ্যাপ থেকে ইমেইল করার অনুমতি চাইবে। অনুমতি দিলেই এর পর থেকে ইমেইল যাবে। তবে এ কারণে নিরাপত্তায় কোনো সমস্যা হলে তার দায় আপনাকেই নিতে হবে!

আরও পড়ুন 
☛ R প্রোগ্রামিং মহান কেন? 

Category: articles

Read More...

বর্তমান পৃথিবী ডেটা বা তথ্য উপাত্ত দিয়ে ভরপুর। সমাজ বা রাষ্ট্রের কার্যকরী পরিকল্পনা ও উন্নয়নের জন্যে চাই বিভিন্ন রকম উপাত্তের সঠিক বিশ্লেষণ। যে কোনো প্রতিষ্ঠান, হোক সেটা আর্থিক, সামাজিক বা গবেষণাধর্মী, সেটাকে ভালোভাবে পরিচালনা ও লক্ষ্যে পৌঁছানোর জন্যে চাই উপাত্ত বিশ্লেষণের মাধ্যমে সঠিক সিদ্ধান্ত গ্রহণ। সেবাদানকারী প্রতিষ্ঠানগুলোকে উপাত্ত ঘেঁটে বুঝতে হয়, কোন পণ্যের বাজার কেমন, মানুষ কোন দিকে ঝুঁকছে ইত্যাদি। গুগোল, ফেসবুকের মতো প্রতিষ্ঠানগুলোর ব্যাবসার অন্যতম বড় উপাদান উপাত্ত বিশ্লেষণ করে ব্যবহারকারীদের আগ্রহ ও ঝোঁক-প্রবণতা অনুমান করা। অ্যামাজন ডট কম, উবার, গুগোলের বিজ্ঞাপন সেবা অ্যাডসেন্স, কিংবা অ্যাপলের সিরি সব কিছুই উপাত্ত বিশ্লেষণের ওপর নির্ভরশীল।  বৈজ্ঞানিক গবেষণার জন্যেও একইভাবে উপাত্তের সঠিক ও গ্রহণযোগ্য ব্যাখ্যা-বিশ্লেষণ প্রয়োজন।

এই যে কাজগুলো, এগুলোর জন্যে বর্তমানে জ্ঞানের নতুন একটু শাখাই গড়ে উঠেছে। নাম ডেটা সায়েন্স। পরিসংখ্যানের ধারণা ও প্রয়োগ নির্ভর জ্ঞানের নতুন এই শাখাটি চাকরির বাজারে ক্রমশ পেছনে ফেলে দিচ্ছে অন্য সব পেশাকে। হার্ভার্ড বিজনেস রিভিউ ম্যাগাজিনের ২০১২ সালের অক্টোবর সংখ্যায় বলা হয়, ‘একুশ শতকের সবচেয়ে আকর্ষণীয় চাকরি হল ডেটা সায়েন্স’। জব রিভিউ সাইট গ্লাসডোর এর একটি জরিপ অনুসারে, ইতোমধ্যে অ্যামেরিকার সেরা পেশার তালিকায় এক নম্বরে স্থান পেয়েছে পেশাটি। আইবিএম এর এক জরিপ অনুসারে শুধু ২০১৫ সালেই অ্যামেরিকায় এই ফিল্ডে সাড়ে তেইশ লাখ চাকরি দেওয়া হয়।

ডেটা সায়েন্সের এ বিশাল ক্ষেত্রটিতে কাজের জন্যে রয়েছে কাড়ি কাড়ি সফটওয়্যার। রয়েছে প্রোগ্রামিং ল্যাঙ্গুয়েজ, স্ট্যাটিস্টিক্যাল প্যাকেজ। অনেকে তো মাইক্রোসফট এক্সেলেই অনেক উপাত্ত বিশ্লেষণ করে ফেলেন। আরেকটু ভালো করতে চাইলে কেউ কেউ আবার SPSS, Stata, Minitab কিংবা SAS এর আশ্রয় গ্রহণ করেন। কেউ কেউ আবার জাভা, পাইথনের মতো প্রোগ্রামিং কাজে লাগিয়েও করেন ডেটা সায়েন্সের কাজ।

তবে সবকিছুকে ছাপিয়ে ডেটা সায়েন্সের জগতে সকল কাজের কাজি হয়ে দাঁড়িয়েছে একটি প্রোগামিং ল্যাঙ্গুয়েজ। নামটি বেশ ছোট: R। রস ইহাকা ও রবার্ট জেন্টেলম্যান নামের দুজন পরিসংখ্যানবিদ এর উদ্ভাবক। কম্পিউটারের হেন কাজ নেই যা ল্যাঙ্গুয়েজটি করতে পারে না। ওয়ার্ড ডকুমেন্ট তৈরি, প্রেজেন্টনেশনের স্লাইড কিংবা পিডিএফ বানানো থেকে শুরু ম্যাপ আঁকা এমনকি ভিডিও এডিটিং সব কিছুতে ওস্তাদ এই ল্যাঙ্গুয়েজ। তবে এর মূল পরিচয় এটি একটি পরিসংখ্যানিক সফটওয়্যার। গ্রাফ এঁকে উপাত্তের চেহারা বোঝা কিংবা বিশ্লেষোণের মাধ্যমে সুন্দর মডেল দাঁড় করানো বা পূর্বাভাস দেওয়া সব কিছুতেই এর জুড়ি মেলা ভার।

সব মিলিয়ে R এর জনপ্রিয়তাও দিন দিন বেড়ে চলছে। নীচের গ্রাফটিতে একটু চোখ বুলালেই বিষয়টি সহজে বোঝা যায়।

চিত্র ১: ২০১৫ ও ২০১৬ সালে উপাত্ত বিশ্লেষণের কাজে প্রোগ্রামিং/পরিসংখ্যানিক ল্যাঙ্গুয়েজের ব্যবহার

কিন্তু R কেন এত জনপ্রিয়? এর পেছনের কারণগুলোতে একটু চোখ বুলিয়ে নেয়া যাক।
প্রথমত, R একটি ফ্রি সফটওয়্যার। Matlab, SPSS কিংবা SAS এর মতো লাইসেন্স ক্রয়ের কোনো বিষয় নেই। যে কেউ ডাউনলোড করে ব্যবহার করতে পারেন। শুধু তাই নয়, এর সোর্স কোডও সবার জন্যে উন্মুক্ত। আপনি চাইলে কোড বদলে একে মডিফাইও করে নিতে পারেন। সাইজও খুব ছোট। মাত্র ৫০ এমবির কাছাকাছি। যেখানে Matlab এর সাইজ ৮ থেকে ১১ জিবি। অন্য দিকে পরিসংখ্যানিক বিশ্লেষণের জন্যে R ই সবচেয়ে পূর্ণাঙ্গ টুল। এর কাজকে একটু সুশৃঙ্খল উপায়ে করার জন্যে রয়েছে আরেকটি সফটওয়্যার R স্টুডিও। দারুণ এই টুলটিও সম্পূর্ণ ফ্রি।

প্রোগ্রামিং/সফটওয়্যার ব্যবহার করতে গেলে মাঝে-মধ্যে সমস্যায় আটকে যাওয়া অস্বাভাবিক নয়। কিন্তু বেশিরভাগ ফ্রি সফটওয়্যারের অসুবিধা হল, সহজে বিভিন্ন সমস্যায় সমাধান পাওয়া যায় না। অথবা সমাধান পেতে হলে গুণতে হয় অর্থ। কিন্তু এখানে সে অসুবিধাও নেই। সমাধানের জন্যে প্রস্তুত আছেন লাখ লাখ ব্যবহারকারীরাই। Stackoverflow কিংবা Quora সহ অসংখ্য ব্লগ ও ফোরামে যে কোন সমস্যা নিয়ে প্রশ্ন করলেই জবাব পাওয়া যায়। দীর্ঘ দিন ধরে R জনপ্রিয় থাকার কারণে বর্তমানে বেশিরভাগ সাধারণ সমস্যার জবাব গুগোলে সার্চ করলে নিমিষেই মিলে যায়। মানে, বেশিরভাগ সমস্যা আগে থেকেই সমাধান হয়েই আছে।

R এর অন্যতম প্রধান একটি সুবিধা হলো অসংখ্য প্যাকেজের উপস্থিতি। ধরুন, আপনি প্রাণপরিসংখ্যান নিয়ে কাজ করতে চান। তাহলে আপনাকে শুধু survivalপ্যাকেজটি লোড করতে হবে। বার ডায়াগ্রাম কিংবা পাই চার্টগুলোকে দৃষ্টিনন্দন করে উপস্থাপন করতে চাইলে আপনার জন্যে ggplot2 নামের প্যাকেজটি। সব মিলিয়ে সুন্দর করে উপাত্ত উপস্থাপনের জন্যে R এর বিকল্প পাওয়া কঠিন। (নীচের চিত্রে R দিয়ে বানানো একটু পাই চার্ট দেখানো হলো।) ডেটাবেজ নিয়ে কাজ করতে চাইলে রয়েছে sqldf। সুন্দর সুন্দর ম্যাপ বানাতে চাইল কাজে আসবে ggmap, maptools সহ অনেকগুলো প্যাকেজ। আর এগুলোও সব কিন্তু বিনামূল্যেই পাওয়া যাবে। এরকম প্যাকেজের সংখ্যা বর্তমানে ১০ হাজারের ওপরে। এগুলো মূল সফটওয়্যারের সাথে না দেয়ার উদ্দেশ্য সফটওয়্যারটি যাতে ভারী না হয়ে যায়। দরকারের সময় ২/৩ ক্লিকেই বা এক লাইন কোড লিখেই লোড করে ফেলা যায় নির্দিষ্ট প্যাকেজটি। নতুন নতুন কাজের জন্যে নিয়মিত নতুন প্যাকেজ উদ্ভাবনের কাজ এখনও চলছেই। এমনকি আপনি নিজেও চাইলে প্যাকেজ বানিয়ে উন্মুক্ত করে দিতে পারেন।

R দিয়ে বানানো পাই চার্ট 

শুধু উপাত্ত বিশ্লেষণের টুল হিসেবেই নয়, অন্যান্য কাজেও ভাগ বসাতে বসাতে R জনপ্রিয় ল্যাঙ্গুয়েজগুলোর তালিকায় ছয়ে স্থান করে নিয়েছে। এখানে (নীচের চিত্র) তুলনা করার সময় মনে রাখতে হবে ডেটা সায়েন্স এর কাজের বাইরে কম্পিউটারের বিশাল একটি ক্ষেত্র রয়েছে। অন্য দিকে ওয়েবসাইট নির্মাণের অন্যতম জনপ্রিয় ভাষা পিএইচপিও কিন্তু R এর পেছনে পড়ে আছে।

আইট্রিপলই (IEEE) এর স্পেকট্রাম ম্যাগাজিনের ২০১৭ সালের জরিপ অনুসারে বিভিন্ন প্রোগ্রামিং এর র‍্যাংকিং

R এর অন্যতম বড় সুবিধা হল, এর ব্যবহারের জন্যে বড় মাপের প্রোগ্রামার হতে হবে না। অল্প কিছু বিষয় শিখে নিয়েই করা যায় অনেক বেশি বিশ্লেষণ। শেখার জন্যে অনলাইনে অসংখ্য টিউটোরিয়ালের (টেক্সট ও ভিডিও দুই সংস্করণেই) পাশাপাশি রয়েছে দারুণ দারুণ অনেক বই। R এর নিজস্ব হেল্প সেকশনেও অনেক কিছু সহজে শিখে নেওয়া সম্ভব।

বিজনেজ অ্যানালাইসিস এর জগতে R এর দক্ষতা বুঝতে পেরে অধিকাংশ প্রচলিত সফটওয়্যারই R এর সাথে সাথে সমন্বয় করে কাজ করার ব্যবস্থা করছে। এছাড়াও এক্সেল, SPSS, Stata, Microsoft Access, Oracle, MySQL কিংবা SQLite দিয়ে বানানো ডেটাবেজও R খুব সহজে পড়ে নিয়ে কাজ করতে পারে।

R এ বানানো গ্রাফ ও ছবি খুব সহজেই ভালো রেজুলেশনের ছবি ও পিডিএফ আকারে সংরক্ষণ করা যায়। উইন্ডোজ, ম্যাকিন্টশ বা লিনাক্স যে কোনো অপারেটিং সিস্টেমেই আর সমান তালে কাজ করতে পটু।

বিজনেস অ্যানালিটিক্স-এ R এর গ্রহণযোগ্যতার কারণে গুগোল, আইবিএম, ফেবসুক, মজিলা, বিং এর মতো প্রতিষ্ঠানগুলো উপাত্ত বিশ্লেষণে ব্যাপকভাবে R ব্যবহার করছে। ক্রিকেট বা ফুটবলের পরিসংখ্যান ঘেঁটে প্রয়োজনীয় ও আকর্ষণীয় তথ্য বের করে আনা ও সেই মাফিক পরিকল্পনা সাজাতেও বর্তমানে R এর ভূমিকা রয়েছে। সব মিলিয়ে R জানা মানে গর্ব করার মতো একটি জিনিসই জানা!

সূত্রঃ
ইডিএক্স ব্লগ, কম্পিউটার ওয়ার্ল্ড ডট কম, ইনফোওয়ার্ল্ড ডট কম, ওয়াশিংটন পোস্ট, আইবিএম ডট কম, স্ট্যাকওভারফ্লো, অ্যানালিটিক্স ট্রেইনিংস ডট কম।

• https://blog.edx.org/the-importance-of-data-science-in-the-21st-century
• analyticstrainings.com/?p=101
• https://www.computerworld.com/article/2921176/business-intelligence/great-r-packages-for-data-import-wrangling-visualization.html
• https://www.analyticsvidhya.com/blog/2016/10/18-new-must-read-books-for-data-scientists-on-r-and-python/
• https://www.infoworld.com/article/2940864/application-development/r-programming-language-statistical-data-analysis.html
• http://sharpsightlabs.com/blog/r-recommend-data-science/
• https://www.washingtonpost.com/news/on-leadership/wp/2016/01/20/glassdoor-ranks-the-25-best-jobs-in-america-2/
• https://www-01.ibm.com/common/ssi/cgi-bin/ssialias?htmlfid=IML14576USEN&
• https://stackoverflow.blog/2017/10/10/impressive-growth-r/
• https://www.kdnuggets.com/2015/05/r-vs-python-data-science.html

Category: articles

Read More...

R এ আঁকা গ্রাফগুলো সাধারণত একটু এবড়োথেবড়ো হয়। অনেক সময়ই দেখতে অতটা সুন্দর হয় না। যেমন এই গ্রাফটি দেখুন।

R প্রোগ্রামিং: টাইম সিরিজ গ্রাফ 

এই ছবিটা কিছুটা এবড়োথেবড়ো। অনেক সময় আরও অনেক বেশি এবড়োথেবড়োও হয়।

সামান্য কিছু কোড করেই একে অনেকটা উন্নত করে নেওয়া যায়।

png(filename="output.png", type="cairo")
#see ?png for more detail
# Code to plot
dev.off()

filename অংশে আপনি যে লোকশনে সেভ করতে চান, সেটা ও ফাইলের নাম উল্লেখ করবেন। উপরের কোডে output নামে একটি png ফাইলে ছবিটা সেভ হবে। আর এটা সেভ হবে আপনার working directory তে। আপনার বর্তমান ওয়ার্কিং ডিরেক্টরি দেখুন।

getwd()

চাইলে আবার পাল্টেও নিতে পারেন।

setwd("D:/R")

উদাহরণ

আমরা নীচের বানানো ডেটা ব্যবহার করব।

x=seq(30000,40000,500)+rnorm(mean=500, sd=1000,n=21)
y=seq(29000,39000,500)+rnorm(mean=500, sd=1000,n=21)
z=x-y
df=data.frame(income=x, expense=y, balance=z
df.ts=ts(df, end=2018)

এবার smooth করার জন্য কাজ। এখানে par(bg="gray") অংশটি অপশনাল। ব্যাকগ্রাউন্ড সেট করার জন্য বসানো হয়েছে।

png(filename="myplot.png", type="cairo")
par(bg="gray")
ts.plot(df.ts, gpars=list(col=topo.colors(3)), lwd=5, ylab="Amount", xlab="Year", main="Smooth R plot")
legend("topleft", legend=names(df), fill=topo.colors(3), ncol=3,)
dev.off()

উপরের ছবিটাই এখন মসৃণ হয়ে এমন হয়ে যাবে।

smooth R প্লট

আরও পড়ুন 

☛ বাহারি ফুলের ডিজাইন

☛ একই প্লটে অনেকগুলো টাইম সিরিজ গ্রাফ

Category: articles

Read More...

লিখেছেনঃ তোফায়েল আজম

ঢাকা বিশ্ববিদ্যালয়ের পরিসংখ্যান বিভাগের ছাত্র ও অ্যালামনাইদের কাছে অন্যতম শ্রদ্ধার নাম কাজী মোতাহার হোসেন স্যার। বাংলাদেশে পরিসংখ্যানের ভিত্তি স্থাপন থেকে শুরু করে পরিসংখ্যানে গবেষনার প্রবাদ পুরুষ হিসেবেই তাকে সবাই শ্রদ্ধার চোখে দেখি।

বাংলাদেশে পরিসংখ্যানের প্রবর্তক মোতাহার হোসেন স্যারের সাথে আধুনিক পরিসংখ্যান বিদ্যার জনক রোনাল্ড ফিশার এর অদ্ভুত মিল। দুইজনই মারাত্মক ব্রিলিয়ান্ট। এতে কোন সন্দেহ কখনো কেউ প্রকাশ করতে পারেনি। অল্প বয়েস থেকেই দুজনই গাণিতিক দৃষ্টির ব্রিলিয়ান্ট ছিলেন।

☛ আরও পড়ুনঃ
রাশিবিজ্ঞান, পরিসংখ্যান ও কাজী মোতাহার হোসেন

রোনাল্ড ফিশার 

দুজনের মধ্যে সবচেয়ে বড়ো মিল ছিল- দুজনই পদার্থবিজ্ঞানের লোক ছিলেন। ঢাকা বিশ্ববিদ্যালয়ে ছিলেন কাজী মোতাহার হোসেন স্যার আর ক্যাম্ব্রিজের এস্ট্রনমির গ্র্যাজুয়েট ছিলেন আর এ ফিশার (১৮৯০-১৯৬২) । পদার্থবিজ্ঞান নিয়ে কাজ করার সময়টায় দুজনই সংখ্যা নিয়ে গবেষণার প্রয়োজনীয়তা অনুভব করেন। ফিশার মশাই উনার জীবনের প্রথম যে পেপার পাবলিশ করেন সেটা স্বাভাবিক ভাবেই ছিল আধুনিক পরিসংখ্যানের জন্য অন্যতম ধাপ- Method of maximum likelihood।

Fisher এরপর কাজ করতে থাকেন W. S. Gosset এর সাথে। বিষয়- Equation of Standard Deviation। এই গবেষণা করতে গিয়েই তিনি Sample mean আর Population mean এর মাঝে দৃশ্যমান পার্থক্যকে গানিতিক ও গঠনমুলক রুপ দান করেন। পরিসংখ্যানের বাস্তব ব্যাবহার নিয়ে এরপর কাজ করতে থাকেন মুলত ছোট ছোট Sample নিয়ে। তখন তিনি Degrees of freedom এর সঙ্গায়ন করেন এবং আরো গভীর গবেষণায় হাত দেন।

ফিশার ব্যক্তিগত ভাবে মারাত্মক গোঁয়ার আর কাজের বেলায় ছিলেন পারফেকশনিস্ট। ভুল করার অপছন্দ থেকেই আরো জোরেসোরে কাজ শুরু করেন সংখ্যান নানান দিক নিয়ে।

১৯১৪ সালে আর্মিতে যোগ দেয়ার জন্য চেষ্টা করেন। কিন্তু ছোটবেলা থেকেই দৃষ্টিত্রুটিতে ভোগা ফিশার আর্মি থেকে রিজেক্টেড হবার পর হাই স্কুলে অংক ও পদার্থ বিজ্ঞান নিয়ে পড়ানো শুরু করার সময় পরিসংখ্যানে চালিয়ে যাওয়া কাজ তখনকার সময়ের বিখ্যাত পরিসংখ্যানবিদ কার্ল পিয়ারসনের নজরে আসেন। ১৯১৭ সালে পিয়ারসন পেপার পাবলিশ করেন ফিশারের কাজের উপর। মূলত ফিশারের method of maximum likelihood এর সমালোচনা সম্বলিত। অল্প নাম ওয়ালা ফিশার বিখ্যাত পিয়ারসনের সমালোচনার জবাব দেন কিন্তু পিয়ারসন তাতে তেমন গা না দিয়ে ফিশারের পরবর্তী অনেক থিওরী ও গবেষণাকে প্রত্যাখ্যান করেন।

সেই সময়টায় ফিশার সংখ্যার এই জগতটায় বাচ্চা, কিন্তু পিয়ারসন স্বনামধন্য। পিয়ারসনের প্রভাবে রয়েল সোসাইটি থেকে ফিশারের প্রায় সব পেপার সরিয়ে নেয়া হয়। কিন্তু পারফেকশনিস্ট ফিশার তাঁর গবেষনা চালিয়ে যান, এবং তার তত্ত্বের পক্ষে প্রমাণ দেন। পিয়ারসন যদিও পরবর্তীতে ফিশারকে তার সাথে কাজ করার জন্য চাকরী অফার করেন, কিন্তু গোঁয়ার ফিশার পিয়ারসনের আগের বিরোধীতার জের ধরে আর সেই চাকরীতে যোগ দেননি! (পরিসংখ্যানের দুই রাইভাল!)

ফিশার তখন পরিসংখ্যানবিদ হিসেবে কাজ শুরু করেন Rothamsted Experimental Station-এ। কাজ করেন কৃষি বিষয়ক গবেষণা নিয়ে এবং Analysis of variance তত্ত্ব দেন এবং কৃষি বিষয়ক গবেষনার ফলাফল হিসেবেই পরবর্তিতে আমরা পাই তার বিখ্যাত Statistical Methods for Research Workers।

১৯১৭তে বিবাহ এবং সংসারী জীবন যাপন করতে থাকা ফিশার পরবর্তীতে কাজ করেন Natural selection and population genetics নিয়ে এবং লিখেন Genetical Theory of Natural Selection। এই বইটায় অবশ্য উনার প্রিয়তমা পত্নি Ruth Eileen লিখতে সাহায্য করেন।

Rothamsted এ কাজ করার সময় ম্যাক্সিমাম লাইকলিহুড এবং সাইন্টিফিক এক্সপেরিমেন্ট থেকে ছোট স্যাম্পল নেবার প্রসেসের উপর আরো দুইখানা গবেষণা প্রকাশ করেন। সেখান থেকেই sample statistic আর population values এর ধারনা স্পষ্ট হতে থাকে। এই দুই পেপার থেকেই বাকি গবেষকেরা নানান ধরনের variations আর প্রিসাইজ এস্টিমেশনের ধরনা পেতে থাকেন।

পিয়ারসন রিটায়ার্ড করার পরে যদিও ফিশার কেম্ব্রিজের চাকরীটা গ্রহন করেন, কিন্তু যুদ্ধটা চলতেই থাকে। এর প্রভাব কেম্ব্রিজ পরিসংখ্যান বিভাগেও পড়ে বৈকি।

দ্বিতীয় বিশ্বযুদ্ধের সময় গবেষণায় বেঘাত ঘটলেও পরবর্তিতে তিনি গবেষণা চালিয়ে যান পরিসংখ্যানের নানান দিক নিয়ে।

সারা জীবনে একটার পর একটা ফেলোশীপ, Iowa state university তে শিক্ষকতা, রয়েল স্ট্যাটিস্টিক্স সোসাইটি থেকে তিনটা মেডেল, ডারউইন মেডেল, কোপলে মেডেল, বিভিন্ন বিশ্ববিদ্যালয় থেকে সম্মান্সূচক ডিগ্রী, ২০টার অধিক ইন্সটিটিট ও একাডেমির সম্মানসূচক সদস্য ১৯৫২ সালে কুইন এলিজাবেথ থেকে নাইট ব্যাচেলর উপাধী গ্রহণ করেন।

ফিশারের গোঁয়ার্তুমি আর পারফেকশনিস্ট আচরণের জন্য আজকের পরিসংখ্যানের এই আধুনিক রূপ। পরবর্তীতে অনেকেই ফিশারের গবেষণার উপর এবং তাঁর দেখানো পথে অভুতপূর্ব কাজ করেছেন। ফিশার পরবর্তী পরিসংখ্যানে তাঁর অভূতপূর্ব অবদানের জন্যই তাঁকে আধুনিক গবেষণার জনক হিসেবে বিবেচনা করা হয়। :)

আজ এই গোঁয়ার লোকটার জন্মদিন। আমাদের সকল কষ্টের(!) জনক এই পদার্থবিদ পরিসংখ্যানের জনককে শুভ জন্মদিন! :)

তথ্যসূত্রঃ 
১। http://mnstats.morris.umn.edu/intro…/history/…/RAFisher.html
২। https://en.wikipedia.org/wiki/Ronald_Fisher

লেখকঃ টিচিং অ্যাসিস্টেন্ট ও পিএইচডি শিক্ষার্থী, ইউনিভার্সিটি অব কেন্টাকি। লেখকের সব লেখা এখানে।

Category: articles

Read More...